Self-organization of domain structures by DNA-loop-extruding enzymes
- PMID: 23074191
- PMCID: PMC3526278
- DOI: 10.1093/nar/gks925
Self-organization of domain structures by DNA-loop-extruding enzymes
Abstract
The long chromosomal DNAs of cells are organized into loop domains much larger in size than individual DNA-binding enzymes, presenting the question of how formation of such structures is controlled. We present a model for generation of defined chromosomal loops, based on molecular machines consisting of two coupled and oppositely directed motile elements which extrude loops from the double helix along which they translocate, while excluding one another sterically. If these machines do not dissociate from DNA (infinite processivity), a disordered, exponential steady-state distribution of small loops is obtained. However, if dissociation and rebinding of the machines occurs at a finite rate (finite processivity), the steady state qualitatively changes to a highly ordered 'stacked' configuration with suppressed fluctuations, organizing a single large, stable loop domain anchored by several machines. The size of the resulting domain can be simply regulated by boundary elements, which halt the progress of the extrusion machines. Possible realizations of these types of molecular machines are discussed, with a major focus on structural maintenance of chromosome complexes and also with discussion of type I restriction enzymes. This mechanism could explain the geometrically uniform folding of eukaryote mitotic chromosomes, through extrusion of pre-programmed loops and concomitant chromosome compaction.
Figures

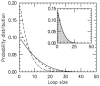
 ) increases. Main figure shows results for
) increases. Main figure shows results for  1.05 (dot-dashed line), 1.5 (dashed line) and 4.0 (solid line). Inset: comparison of steady-state loop-size distributions for exact statistical theory (solid black line) and kinetic simulation
1.05 (dot-dashed line), 1.5 (dashed line) and 4.0 (solid line). Inset: comparison of steady-state loop-size distributions for exact statistical theory (solid black line) and kinetic simulation  (gray bars); difference between them is negligibly small. The simulation was run
(gray bars); difference between them is negligibly small. The simulation was run  times, each for a time of
times, each for a time of  Standard errors for the histogram bars have a maximum value of
Standard errors for the histogram bars have a maximum value of  and are invisible on this plot.
and are invisible on this plot.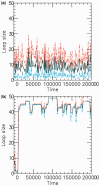
 for a (a) non-disassociating and a (b) dissociating case (
for a (a) non-disassociating and a (b) dissociating case ( ), for M = 5 machines on a substrate of length L = 50. The dark solid line shows the average of the sizes of the M loops, and the red and blue dashed lines indicate the width (one standard deviation) of the distribution of loop sizes subtended by the machines as a function of time. As in all cases mentioned in this article, time is in units of
), for M = 5 machines on a substrate of length L = 50. The dark solid line shows the average of the sizes of the M loops, and the red and blue dashed lines indicate the width (one standard deviation) of the distribution of loop sizes subtended by the machines as a function of time. As in all cases mentioned in this article, time is in units of  .
.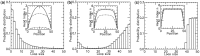
 for different motor biases
for different motor biases  (a), 1.50 (b) and 4.00 (c). Panels (a–c) show loop-size distributions for the simulation steady state: as bias is increased, a peak grows at
(a), 1.50 (b) and 4.00 (c). Panels (a–c) show loop-size distributions for the simulation steady state: as bias is increased, a peak grows at  as motor pairs begin to trap the entire domain. Each panel was computed using
as motor pairs begin to trap the entire domain. Each panel was computed using  simulations each of total time
simulations each of total time  The maximum size of the standard error bars for the histograms are
The maximum size of the standard error bars for the histograms are  and
and  for panels (a)–(c), respectively. The insets show the motor position (labeled ‘head index’) index
for panels (a)–(c), respectively. The insets show the motor position (labeled ‘head index’) index  along the lattice: dashed lines show the average ( 1 SD for the simulations (standard error bars for the insets are invisible on this plot); solid curves show average obtained from approximate effective Boltzmann description of the steady state. As bias is increased, fluctuations are suppressed and the motors become ‘stacked’.
along the lattice: dashed lines show the average ( 1 SD for the simulations (standard error bars for the insets are invisible on this plot); solid curves show average obtained from approximate effective Boltzmann description of the steady state. As bias is increased, fluctuations are suppressed and the motors become ‘stacked’.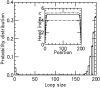
 , and M = 5 motor pairs. The simulation was run
, and M = 5 motor pairs. The simulation was run  times, each for a time of
times, each for a time of  The maximum size of the standard error bars is
The maximum size of the standard error bars is  For the
For the  profile (inset, labeled ‘head index’), the solid line is the effective Boltzmann theory, dashed lines show average ± 1 SD of the simulation
profile (inset, labeled ‘head index’), the solid line is the effective Boltzmann theory, dashed lines show average ± 1 SD of the simulation  distribution; standard errors of the simulation results are negligibly small. Dissociation rate is
distribution; standard errors of the simulation results are negligibly small. Dissociation rate is  .
.

References
-
- Nielsen HJ, Ottesen JR, Youngren B, Austin SJ, Hansen FG. The Escherichia coli chromosome is organized with the left and right chromosome arms in separate cell halves. Mol. Microbiol. 2006;62:331–338. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

