Quantifying the behavior of stock correlations under market stress

Abstract

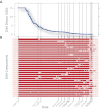
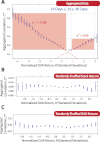
Understanding correlations in complex systems is crucial in the face of turbulence, such as the ongoing financial crisis. However, in complex systems, such as financial systems, correlations are not constant but instead vary in time. Here we address the question of quantifying state-dependent correlations in stock markets. Reliable estimates of correlations are absolutely necessary to protect a portfolio. We analyze 72 years of daily closing prices of the 30 stocks forming the Dow Jones Industrial Average (DJIA). We find the striking result that the average correlation among these stocks scales linearly with market stress reflected by normalized DJIA index returns on various time scales. Consequently, the diversification effect which should protect a portfolio melts away in times of market losses, just when it would most urgently be needed. Our empirical analysis is consistent with the interesting possibility that one could anticipate diversification breakdowns, guiding the design of protected portfolios.

Figure 1. Index components of the Dow Jones Industrial Average (DJIA).

(A) To calculate the index value of the DJIA, we determine the sum of prices of all 30 stocks belonging to the index and divide them by the depicted “DJIA Divisor”. Adjustments of this divisor ensure that various corporate actions such as stock splits do not affect the index value. (B) We analyze DJIA values and prices of all index components for 72 years from March 15, 1939 until December 31, 2010. Vertical dashed lines correspond to events in which at least one stock was removed from the index and replaced by another stock. The index changes are explicitly taken into account to ensure that the dataset, comprising 18,596 trading days, accurately reflects all 30 daily closing prices needed for the index calculation. We use current and historical ticker symbols to abbreviate company names.

Figure 2. Visualization of the analysis method.

(A) For a time interval of Δt trading days, we calculate for the index the price return log(p_DJIA(t + Δt))/log(p_DJIA(t)) in this interval. (B) We determine the Pearson correlation coefficients of all pairs of all 30 DJIA components depicted in a matrix of correlation coefficients. Ticker symbols are used to abbreviate company names in this example. We calculate the mean correlation coefficient by averaging over all non-diagonal elements of this matrix.

Figure 3. Quantification of state-dependent correlations among index components.

(A) Graphs reflect the relationship between the average correlation coefficient C among stocks belonging to the Dow Jones Industrial Average and its normalized return in intervals of Δt trading days. The mean correlation coefficient shows a striking, non-constant behavior, with a minimum between 0 and +1 standard deviations reflecting typical market conditions. For the range of all Δt values analyzed, we find the data collapse onto a single line. Corresponding error bars are shown in Fig. 4A. The data collapse suggests that the striking increase of the mean correlation coefficient for positive and negative values of the normalized index return is independent of the time interval Δt. The largest mean correlation coefficients coincide with the most negative index returns. (B) Normalized DJIA returns, R(t, Δt), and mean correlation coefficients, C(t, Δt), shown for Δt = 10 days. For both time series, we reject the null hypothesis of non-stationarity on the basis of results from the Augmented Dickey-Fuller test. For R(t, Δt = 10), we obtain DF = −24.28, p < 0.01, while for C(t, Δt = 10) we obtain DF = −13.45, p < 0.01.

Figure 4. Quantification of the aggregated correlation.

(A) Utilizing the data collapse reported in Fig. 3, we aggregate in each bin of the graph the mean correlation coefficients for 10 days ≤ Δt ≤ 60 days. Error bars are plotted depicting −1 and +1 standard deviations around the mean of the mean correlation values included in each bin. The increase of the aggregated correlation C* for positive and negative index returns is consistent with two linear relationships: C* = a⁺R + b⁺ with a⁺ = 0.064 ± 0.002 and b⁺ = 0.188 ± 0.004 (p – value < 0.001) quantifies the right part. C* = a⁻R + b⁻ with a⁻ = −0.085 ± 0.002 and b⁻ = 0.267 ± 0.005 (p – value < 0.001). The red colored regions are used to obtain the coefficients. In order to reduce noise, the range of normalized DJIA returns is restricted to bin values occurring, on average, more than 10 times for individual Δt intervals. (B) By randomly shuffling time series of daily returns for each stock individually, we test the robustness of the relationship and find that the linear relationships reported in (A) disappear, supporting our findings. (C) We use non-shuffled time series of underlying stock returns for an additional parallel analysis with randomly shuffled DJIA returns. The above linear relationships also vanish in this test scenario underlining the robustness of our findings.