On the role of CD8 T cells in the control of persistent infections
- PMID: 23083724
- PMCID: PMC3475343
- DOI: 10.1016/j.bpj.2012.07.059
On the role of CD8 T cells in the control of persistent infections
Abstract
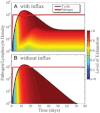
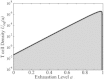
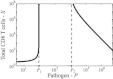
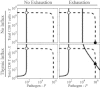
The control of pathogen density during infections is typically assumed to be the result of a combination of resource limitation (loss of target cells that the pathogen can infect), innate immunity, and specific immunity. The contributions of these factors have been considered in acute infections, which are characterized by having a short duration. What controls the pathogen during persistent infections is less clear, and is complicated by two factors. First, specific immune responses become exhausted if they are subject to chronic stimulation. Exhaustion has been best characterized for CD8 T cell responses, and occurs through a combination of cell death and loss of functionality of surviving cells. Second, new nonexhausted T cells can immigrate from the thymus during the infection, and may play a role in the control of the infection. In this article, we formulate a partial-differential-equation model to describe the interaction between these processes, and use this model to explore how thymic influx and exhaustion might affect the ability of CD8 T cell responses to control persistent infections. We find that although thymic influx can play a critical role in the maintenance of a limited CD8 T cell response during persistent infections, this response is not sufficiently large to play a significant role in controlling the infection. In doing so, our results highlight the importance of resource limitation and innate immunity in the control of persistent infections.
Copyright © 2012 Biophysical Society. Published by Elsevier Inc. All rights reserved.
Figures

References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials

