Microsatellites as targets of natural selection

Abstract

The ability to survey polymorphism on a genomic scale has enabled genome-wide scans for the targets of natural selection. Theory that connects patterns of genetic variation to evidence of natural selection most often assumes a diallelic locus and no recurrent mutation. Although these assumptions are suitable to selection that targets single nucleotide variants, fundamentally different types of mutation generate abundant polymorphism in genomes. Moreover, recent empirical results suggest that mutationally complex, multiallelic loci including microsatellites and copy number variants are sometimes targeted by natural selection. Given their abundance, the lack of inference methods tailored to the mutational peculiarities of these types of loci represents a notable gap in our ability to interrogate genomes for signatures of natural selection. Previous theoretical investigations of mutation-selection balance at multiallelic loci include assumptions that limit their application to inference from empirical data. Focusing on microsatellites, we assess the dynamics and population-level consequences of selection targeting mutationally complex variants. We develop general models of a multiallelic fitness surface, a realistic model of microsatellite mutation, and an efficient simulation algorithm. Using these tools, we explore mutation-selection-drift equilibrium at microsatellites and investigate the mutational history and selective regime of the microsatellite that causes Friedreich's ataxia. We characterize microsatellite selective events by their duration and cost, note similarities to sweeps from standing point variation, and conclude that it is premature to label microsatellites as ubiquitous agents of efficient adaptive change. Together, our models and simulation algorithm provide a powerful framework for statistical inference, which can be used to test the neutrality of microsatellites and other multiallelic variants.

Fig. 1.

Modeling mutation and selection at a microsatellite. (A) The diploid fitness surface is constructed in two steps. First, allelic fitnesses are calculated by combining the threshold and gradient effects associated with the values of parameters δ, g_l, and g_u. Second, the vector of allelic fitnesses is used to compute the fitness surface (genotypic fitnesses) in a model-specific manner. (B) Allele-specific mutation rate is defined as a basic logistic function modified by three parameters whose values control the allele size where mutation rate begins to increase (ψ), the slope of increase (γ), and the maximum mutation rate (ϕ).

Fig. 2.

Mutation-selection-drift equilibrium for a microsatellite under selection. (A) The joint distribution of key allele (size = 8) frequency versus time for 1,000 replicates at a selected microsatellite locus. In this case, the key allele is also the most fit and its frequency at mutation-selection equilibrium is 0.9684 (dashed line). The simulated selective regime was dominant model with x = 8, δ = 0.05, g_l = −0.001, and g_u = 0. Simulated mutational parameters were ϕ = 3.5, ψ = 1.5, γ = 0.15, m = 1, and c = 0. Diploid population size N_e = 10,000. (B) The same as (A) for 1,000 simulations where N_e = 500. (C) Derived from the same simulations as (A), the joint distribution of the frequency of allele size 7 versus time is shown. This allele is the next most-fit allele according to the modeled selective regime. (D) The fitness surface used in the simulations underlying (A–C).

Fig. 3.

The demographic model for FRDA inference. Outer trees indicate population size. Inner shaded trees represent the frequencies of LN and E class alleles. Parameters t_b (bottleneck time) and t_e (time of LN class origin) were drawn from uniform prior distributions before the start of each simulation. The relationship between these parameter values distinguished between two historical possibilities. 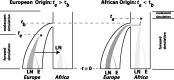When (left), the bottleneck occurred before the emergence of the first LN allele. In this case, the LN and E alleles observed in Northern Africa on the same haplotypic background as European LN and E alleles can only be explained by back-migration to Africa (arrow). When (right), LN emergence takes place in Africa and is subsequently carried to Europe by members of a founding population. Note that only simulations where LN alleles survived to modern day (t = 0) were retained and that the postdivergence African population was not simulated. Coalescent simulation was used to simulate starting distributions of genetic variation; forward simulations as detailed here were used to progress from time t_e to t = 0.

Fig. 4.

Estimate of the fitness surface for the GAA repeat that causes Friedreich’s ataxia. This estimate is based on median selective parameter values from their posterior distributions. The solid black lines are drawn at allele size 34. We assumed that all genotypes with at least one allele of size <34 had a relative fitness of 1. The least fit genotype on the graph, 1,500/1,500, has an estimated fitness of only 0.104.

Fig. 5.

Cost and duration of microsatellite selection. (A) Regression of log C on Δ_msat for additive regimes A1 and A2 (table 2). The results of 250 deterministic simulations are shown. The only difference between replicates of the same regime was the starting distribution of allele frequencies, which was generated using neutral coalescent simulation. Δ_msat quantifies the difference between starting allele frequencies and those at mutation-selection balance. Best fit lines for both regimes are drawn. (B) Duration of selection versus cost of selection for regimes R1, D1, A2, and M2; 250 deterministic replicates each. The dashed line is drawn from deterministic simulations of a hard, SNP-based selective sweep (dominance coefficient h = 0.5). The line is interpolated but based on thousands of simulations, each with a different value of s. Two values of s are indicated on the dashed line.

Fig. 6.

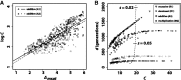
Results from 250 independent simulations each of additive selection on a microsatellite, a soft sweep (p₀ on the interval [0.1, 0.2]), or a hard sweep (), where p₀ is the starting frequency of the beneficial SNP variant. The y-axis plots , where final nucleotide diversity () was calculated from a sample of n = 100 chromosomes either at the time of fixation of the beneficial variant (SNP selection) or when mutation-selection-drift equilibrium was achieved (microsatellite selection). In all selection scenarios, the target of selection was located at the center of a 1 Mb sequence. Box plots summarize the results from simulations of microsatellite selection in non-overlapping 10 kb windows (rectangles are interquartile distances). Colored lines plot the mean value of across simulations for soft sweep (orange) and hard sweep (blue) simulations.