Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2012 Oct 29;7(1):597.
doi: 10.1186/1556-276X-7-597.

Mechanical properties of sintered meso-porous silicon: a numerical model

Roberto Martini  1 , Valerie Depauw, Mario Gonzalez, Kris Vanstreels, Kris Van Nieuwenhuysen, Ivan Gordon, Jef Poortmans
Affiliations

Mechanical properties of sintered meso-porous silicon: a numerical model

Roberto Martini et al. Nanoscale Res Lett. .

Abstract

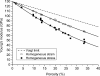
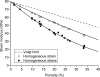
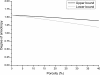
: Because of its optical and electrical properties, large surfaces, and compatibility with standard silicon processes, porous silicon is a very interesting material in photovoltaic and microelectromechanical systems technology. In some applications, porous silicon is annealed at high temperature and, consequently, the cylindrical pores that are generated by anodization or stain etching reorganize into randomly distributed closed sphere-like pores. Although the design of devices which involve this material needs an accurate evaluation of its mechanical properties, only few researchers have studied the mechanical properties of porous silicon, and no data are nowadays available on the mechanical properties of sintered porous silicon. In this work we propose a finite element model to estimate the mechanical properties of sintered meso-porous silicon. The model has been employed to study the dependence of the Young's modulus and the shear modulus (upper and lower bounds) on the porosity for porosities between 0% to 40%. Interpolation functions for the Young's modulus and shear modulus have been obtained, and the results show good agreement with the data reported for other porous media. A Monte Carlo simulation has also been employed to study the effect of the actual microstructure on the mechanical properties.

PubMed Disclaimer

Figures

Figure 1
Figure 1
SEM picture of a sintered PSi cross section. SEM picture of sintered meso-PSi after 20 min annealing in H2 atmosphere at 1,100°C and 1 atm.
Figure 2
Figure 2
Example of RVE. Example of RVE employed for the study of the overall mechanical properties of porous silicon and two cross-sections.
Figure 3
Figure 3
PSi Young’s modulus as function of porosity. Numerical results for uniform displacements (empty squares) and uniform traction (full squares) conditions and interpolations (solid line) representing the upper and lower bounds of the homogenized Young’s modulus as function of porosity. Curves are always underneath the Voigt theoretical upper bound (dashed line).
Figure 4
Figure 4
PSi shear modulus as function of porosity. Numerical results for uniform displacements (empty squares) and uniform traction (full squares) conditions and interpolations (solid line) representing the upper and lower bounds of the homogenized shear modulus as function of porosity. Curves are always underneath the Voigt theoretical upper bound (dashed line).
Figure 5
Figure 5
PSi degree of anisotropy as function of porosity. Degree of anisotropy computed as G(Ψ)2(1+ν(Ψ))E(Ψ) for both the upper and lower bounds as function of porosity.
Figure 6
Figure 6
Statistical distribution of PSi Young’s modulus and shear modulus. Statistical distribution of PSi Young’s modulus (left) and shear modulus (right) obtained by Monte Carlo simulations. The mean value and the standard deviation are reported in the legend.
See this image and copyright information in PMC

References

    1. Brendel R. Thin-film crystalline silicon mini-modules using porous Si for layer transfer. Sol Energy. 2004;77(6):969–982. doi: 10.1016/j.solener.2004.08.011. - DOI
    1. Bellet D, Lamagnere P, Vincent A, Brechet Y. Nanoindentation investigation of the Young’s modulus of porous silicon. J Appl Phys. 1996;80(7):3772–3776. doi: 10.1063/1.363305. - DOI
    1. Andrews GT, Zuk J, Kiefte H, Clouter MJ, Nossarzewska-Orlowska E. Elastic characterization of a supported porous silicon layer by Brillouin scattering. Appl Phys Lett. 1996;69(9):1217–1219. doi: 10.1063/1.117416. - DOI
    1. Cho H, Sato H, Nishino H, Tsukahara Y, Inaba M, Sato A, Takemoto M, Nakano S, Yamanaka K. Proceedings of IEEE Ultrasonics Symposium Volume 1: November 7-10 1995, Cannes. IEEE Xplore, Piscataway; 1995. Nondestructive evaluation of elastic properties in porous silicon film on Si(100) by the phase velocity scanning of laser interference fringes; pp. 757–760.
    1. Fonseca RJM, Saurel JM, Foucaran A, Camassel J, Massone E, Taliercio T, Boumaiza Y. Acoustic investigation of porous silicon layers. J Mater Sci. 1995;30:35–39. doi: 10.1007/BF00352128. - DOI

LinkOut - more resources