ChopSticks: High-resolution analysis of homozygous deletions by exploiting concordant read pairs
- PMID: 23110596
- PMCID: PMC3582528
- DOI: 10.1186/1471-2105-13-279
ChopSticks: High-resolution analysis of homozygous deletions by exploiting concordant read pairs
Abstract
Background: Structural variations (SVs) in genomes are commonly observed even in healthy individuals and play key roles in biological functions. To understand their functional impact or to infer molecular mechanisms of SVs, they have to be characterized with the maximum resolution. However, high-resolution analysis is a difficult task because it requires investigation of the complex structures involved in an enormous number of alignments of next-generation sequencing (NGS) reads and genome sequences that contain errors.
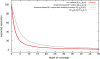
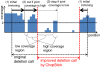
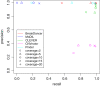
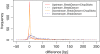
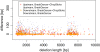
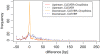
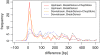
Results: We propose a new method called ChopSticks that improves the resolution of SV detection for homozygous deletions even when the depth of coverage is low. Conventional methods based on read pairs use only discordant pairs to localize the positions of deletions, where a discordant pair is a read pair whose alignment has an aberrant strand or distance. In contrast, our method exploits concordant reads as well. We theoretically proved that when the depth of coverage approaches zero or infinity, the expected resolution of our method is asymptotically equal to that of methods based only on discordant pairs under double coverage. To confirm the effectiveness of ChopSticks, we conducted computational experiments against both simulated NGS reads and real NGS sequences. The resolution of deletion calls by other methods was significantly improved, thus demonstrating the usefulness of ChopSticks.
Conclusions: ChopSticks can generate high-resolution deletion calls of homozygous deletions using information independent of other methods, and it is therefore useful to examine the functional impact of SVs or to infer SV generation mechanisms.
Figures
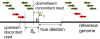









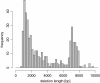
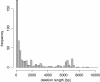
References
-
- Illumina Sequencing portfolio. [ http://www.illumina.com/systems/sequencing.ilmn]
-
- Mills RE, Walter K, Stewart C, Handsaker RE, Chen K, Alkan C, Abyzov A, Yoon SC, Ye K, Cheetham RK, Chinwalla A, Conrad DF, Fu Y, Grubert F, Hajirasouliha I, Hormozdiari F, Iakoucheva LM, Iqbal Z, Kang S, Kidd JM, Konkel MK, Korn J, Khurana E, Kural D, Lam HYK, Leng J, Li R, Li Y, Lin CY, Luo R. et al. 1000 genomes project: Mapping copy number variation by population-scale genome sequencing. Nature. 2011;470:59–65. doi: 10.1038/nature09708. - DOI - PMC - PubMed
-
- Medvedev P, Stanciu M, Brudno M. Computational methods for discovering structural variation with next-generation sequencing. Nat Methods. 2009;6:S13—S20. - PubMed
-
- Chen K, Wallis JW, McLellan MD, Larson DE, Kalicki JM, Pohl CS, McGrath SD, Wendl MC, Zhang Q, Locke DP, Shi X, Fulton RS, Ley TJ, Wilson RK, Ding L, Mardis ER. BreakDancer: an algorithm for high-resolution mapping of genomic structural variation. Nat Methods. 2009;6:677–681. doi: 10.1038/nmeth.1363. - DOI - PMC - PubMed
MeSH terms
LinkOut - more resources
Full Text Sources

