Open source software for electric field Monte Carlo simulation of coherent backscattering in biological media containing birefringence

Abstract

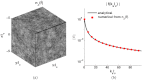
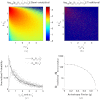
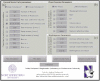
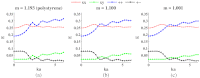
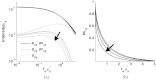
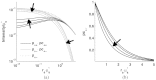
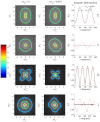
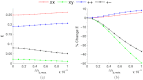
ABSTRACT. We present an open source electric field tracking Monte Carlo program to model backscattering in biological media containing birefringence, with computation of the coherent backscattering phenomenon as an example. These simulations enable the modeling of tissue scattering as a statistically homogeneous continuous random media under the Whittle-Matérn model, which includes the Henyey-Greenstein phase function as a special case, or as a composition of discrete spherical scatterers under Mie theory. The calculation of the amplitude scattering matrix for the above two cases as well as the implementation of birefringence using the Jones N-matrix formalism is presented. For ease of operator use and data processing, our simulation incorporates a graphical user interface written in MATLAB to interact with the underlying C code. Additionally, an increase in computational speed is achieved through implementation of message passing interface and the semi-analytical approach. Finally, we provide demonstrations of the results of our simulation for purely scattering media and scattering media containing linear birefringence.

Fig. 1

Numerical validation of our treatment of scattering using function ${\mathit{M}}_n(r)$. (a) Randomly generated 3-D medium under the Whittle-Matérn model for $D=3$. (b) Comparison of function $|f|$ calculated numerically and analytically for the medium shown in panel a.

Fig. 2

Comparison between the semi-analytical and traditional Monte Carlo method in a sample of Rayleigh scatterers simulated for the $xx$ polarization channel. Function $p_{xx}(r_s·{\mu }_s^{*},z·{\mu }_s^{*})$ for (a) the semi-analytical method and (b) the traditional method. (c) Functions $p_{xx}(r_s·{\mu }_s^{*})$ and $p_{xx}(z_s·{\mu }_s^{*})$ achieved by summing $p_{xx}(r_s·{\mu }_s^{*},z·{\mu }_s^{*})$ over rows and columns, respectively. The symbols indicate the traditional technique while the solid line indicates the semi-analytical approach. (d) Computational efficiency measured by taking the ratio of the number of traditional photons over the number of semi-analytical photons needed to achieve the same simulation noise level. These simulations utilize the Whittle-Matérn model with $D=3$.

Fig. 3

MATLAB GUI for performing Monte Carlo simulations of CBS. (a) Specification of the general Monte Carlo parameters. (b) Specification of scattering model to be implemented. (c) Specification of the birefringence properties of the sample.

Fig. 4

Enhancement factor $E$ versus size parameter $ka$ for various polarization channels under Mie theory. (a) Trends for relative refractive index $m=n_{\text{sphere}}/n_{\text{medium}}$ corresponding to aqueous suspension of polystyrene microspheres. (b) Trends for $m=1.1$. (c) Trends for $m=1.001$.

Fig. 5

Enhancement factor $E$ versus $k{l}_c$ for various polarization channels under the Whittle-Matérn model. (a) Trends for $D=2$. (b) Trends for $D=3$. (c) Trends for $D=4$.

Fig. 6

Effects of linear birefringence on the spatial reflectance profiles under linear polarized illumination and collection for a sample of Rayleigh scatterers. (a) The normalized intensity distributions $p_{xx}·{pc}_{xx}$ and $p_{xy}·{pc}_{xy}$ which are measurable using CBS. The dashed line indicates the shape of the incoherent $p_{xy}$ distribution which is not directly measurable using CBS. (b) Function ${pc}_{xy}$. Due to the full reversibility of the $xx$ polarization channel, ${pc}_{xx}=1$ for all length-scales. In both panels, the arrow indicates increasing $\mathrm{\Delta }{n}_{b,\max }=0$, $4\times {10}^{-4}$, $7\times {10}^{-4}$, and $1\times {10}^{-3}$.

Fig. 7

Effects of linear birefringence on the spatial reflectance profiles under circularly polarized illumination and collection for a sample of Rayleigh scatterers. (a) The normalized intensity distributions $p_{++}·{pc}_{++}$ and $p_{+-}·{pc}_{+-}$ which are measurable using CBS. The dashed line indicates the shape of the incoherent $p_{+-}$ distribution which is not directly measurable using CBS. (b) Function ${pc}_{+-}$. Due to the full reversibility of the $++$ polarization channel, ${pc}_{++}=1$ for all length-scales. In both panels, the arrow indicates increasing $\mathrm{\Delta }{n}_{b,\max }=0$, $4\times {10}^{-4}$, $7\times {10}^{-4}$, and $1\times {10}^{-3}$.

Fig. 8

Alterations in the shape of $p(x_s,y_s)·pc(x_s,y_s)$ due to birefringence for different polarization channels. To emphasize the shape of the various distributions, each image shows ${\log }_{10}[p(x_s,y_s)·pc(x_s,y_s)]$ in the same intensity scale. (Rows) Each row corresponds to the polarization channel specified on the far right of the figure: top row shows $xx$ polarization, second row shows $++$ polarization, third row shows $xy$ polarization, and the bottom row shows $+-$ polarization. (Columns) The left column shows the ${\log }_{10}[p(x_s,y_s)·pc(x_s,y_s)]$ distributions for $\mathrm{\Delta }{n}_{b,\max }=0$ and the middle column shows the distributions for $\mathrm{\Delta }{n}_{b,\max }=1\times {10}^{-3}$. The right column shows the angular distribution found by converting to polar coordinates, summing over radius, and normalizing by the mean.

Fig. 9

Changes in $E$ as a function of $\mathrm{\Delta }{n}_{b,\max }$ for various polarization channels. (a) Trends of versus $E$. (b) Percent change in $E$ from the absence of birefringence case versus $\mathrm{\Delta }{n}_{b,\max }$.