Phenomenological model for predicting the catabolic potential of an arbitrary nutrient
- PMID: 23133365
- PMCID: PMC3486842
- DOI: 10.1371/journal.pcbi.1002762
Phenomenological model for predicting the catabolic potential of an arbitrary nutrient
Abstract
The ability of microbial species to consume compounds found in the environment to generate commercially-valuable products has long been exploited by humanity. The untapped, staggering diversity of microbial organisms offers a wealth of potential resources for tackling medical, environmental, and energy challenges. Understanding microbial metabolism will be crucial to many of these potential applications. Thermodynamically-feasible metabolic reconstructions can be used, under some conditions, to predict the growth rate of certain microbes using constraint-based methods. While these reconstructions are powerful, they are still cumbersome to build and, because of the complexity of metabolic networks, it is hard for researchers to gain from these reconstructions an understanding of why a certain nutrient yields a given growth rate for a given microbe. Here, we present a simple model of biomass production that accurately reproduces the predictions of thermodynamically-feasible metabolic reconstructions. Our model makes use of only: i) a nutrient's structure and function, ii) the presence of a small number of enzymes in the organism, and iii) the carbon flow in pathways that catabolize nutrients. When applied to test organisms, our model allows us to predict whether a nutrient can be a carbon source with an accuracy of about 90% with respect to in silico experiments. In addition, our model provides excellent predictions of whether a medium will produce more or less growth than another (p<10(-6)) and good predictions of the actual value of the in silico biomass production.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

 it can produce in species s when acting as the sole source of carbon? We find that
it can produce in species s when acting as the sole source of carbon? We find that  is proportional to Ci, the number of carbons in nutrient i, and that the proportionality constant y
s depends on the species s. iii) What is the maximal biomass production B
m(m) when growing on a complex medium m? We find that B
m(m) can be well approximated by adding up the individual contributions
is proportional to Ci, the number of carbons in nutrient i, and that the proportionality constant y
s depends on the species s. iii) What is the maximal biomass production B
m(m) when growing on a complex medium m? We find that B
m(m) can be well approximated by adding up the individual contributions  of nutrients i present in medium m.
of nutrients i present in medium m.




 (see text) for all the sugars uptaken by species s. S. aureus exhibits a reduced biomass production; the biomass defined in the in silico organisms demands approximately ten times more moles relative to the other species. In all the plots, the position of the nutrients on the X axis is slightly staggered so that all data points are visible. Note that the symbols for the complex nutrients are enlarged.
(see text) for all the sugars uptaken by species s. S. aureus exhibits a reduced biomass production; the biomass defined in the in silico organisms demands approximately ten times more moles relative to the other species. In all the plots, the position of the nutrients on the X axis is slightly staggered so that all data points are visible. Note that the symbols for the complex nutrients are enlarged.
 of G nutrients for species in the training set (left) and in the test set (right). Nutrients are grouped by their nutrient class (with positions in the X axis staggered so as to allow one to see all of them). The blue line represents
of G nutrients for species in the training set (left) and in the test set (right). Nutrients are grouped by their nutrient class (with positions in the X axis staggered so as to allow one to see all of them). The blue line represents  for all the sugars uptaken by species s. The symbols for complex nutrients are enlarged.
for all the sugars uptaken by species s. The symbols for complex nutrients are enlarged.
 (see Text and Methods). Additionally, for each nutrient class that contains these nutrients, we show the mean and variance.
(see Text and Methods). Additionally, for each nutrient class that contains these nutrients, we show the mean and variance.
 . We obtain: K = 0.76 for E. coli, K = 0.62 for B. subtilis, K = 0.84 for S. cerevisiae, K = 1.10 for H. pylori, and K = 0.92 for M. tuberculosis.
. We obtain: K = 0.76 for E. coli, K = 0.62 for B. subtilis, K = 0.84 for S. cerevisiae, K = 1.10 for H. pylori, and K = 0.92 for M. tuberculosis.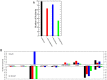

Similar articles
-
From bit to it: how a complex metabolic network transforms information into living matter.BMC Syst Biol. 2007 Jul 30;1:33. doi: 10.1186/1752-0509-1-33. BMC Syst Biol. 2007. PMID: 17663759 Free PMC article.
-
Continuous modeling of metabolic networks with gene regulation in yeast and in vivo determination of rate parameters.Biotechnol Bioeng. 2012 Sep;109(9):2325-39. doi: 10.1002/bit.24503. Epub 2012 Apr 24. Biotechnol Bioeng. 2012. PMID: 22447363
-
Steady-state and dynamic flux balance analysis of ethanol production by Saccharomyces cerevisiae.IET Syst Biol. 2009 May;3(3):167-79. doi: 10.1049/iet-syb.2008.0103. IET Syst Biol. 2009. PMID: 19449977
-
A new thermodynamically based correlation of chemotrophic biomass yields.Antonie Van Leeuwenhoek. 1991 Oct-Nov;60(3-4):235-56. doi: 10.1007/BF00430368. Antonie Van Leeuwenhoek. 1991. PMID: 1807196 Review.
-
A systems biology approach to studying the role of microbes in human health.Curr Opin Biotechnol. 2013 Feb;24(1):4-12. doi: 10.1016/j.copbio.2012.10.001. Epub 2012 Oct 25. Curr Opin Biotechnol. 2013. PMID: 23102866 Review.
Cited by
-
Scaling and optimal synergy: Two principles determining microbial growth in complex media.Phys Rev E Stat Nonlin Soft Matter Phys. 2015 Jun;91(6):062703. doi: 10.1103/PhysRevE.91.062703. Epub 2015 Jun 8. Phys Rev E Stat Nonlin Soft Matter Phys. 2015. PMID: 26172732 Free PMC article.
References
-
- Stephanopoulos G (2007) Challenges in engineering microbes for biofuels production. Science 315: 801–804. - PubMed
-
- Timmis KN, Steffan RJ, Unterman R (1994) Designing microorganisms for the treatment of toxic wastes. Annual Review of Microbiology 48: 525–557. - PubMed
-
- Faulwetter JL, Gagnon V, Sundberg C, Chazarenc F, Burr MD, et al. (2009) Microbial processes influencing performance of treatment wetlands: A review. Ecological Engineering 35: 987–1004.
-
- Keasling JD (2010) Manufacturing molecules through metabolic engineering. Science 330: 1355–1358. - PubMed
-
- Levine AJ, Puzio-Kuter AM (2010) The control of the metabolic switch in cancers by oncogenes and tumor suppressor genes. Science 330: 1340–1344. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

