Principles for designing ideal protein structures
- PMID: 23135467
- PMCID: PMC3705962
- DOI: 10.1038/nature11600
Principles for designing ideal protein structures
Abstract
Unlike random heteropolymers, natural proteins fold into unique ordered structures. Understanding how these are encoded in amino-acid sequences is complicated by energetically unfavourable non-ideal features--for example kinked α-helices, bulged β-strands, strained loops and buried polar groups--that arise in proteins from evolutionary selection for biological function or from neutral drift. Here we describe an approach to designing ideal protein structures stabilized by completely consistent local and non-local interactions. The approach is based on a set of rules relating secondary structure patterns to protein tertiary motifs, which make possible the design of funnel-shaped protein folding energy landscapes leading into the target folded state. Guided by these rules, we designed sequences predicted to fold into ideal protein structures consisting of α-helices, β-strands and minimal loops. Designs for five different topologies were found to be monomeric and very stable and to adopt structures in solution nearly identical to the computational models. These results illuminate how the folding funnels of natural proteins arise and provide the foundation for engineering a new generation of functional proteins free from natural evolution.
Figures
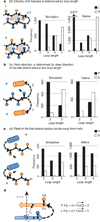

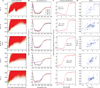

Comment in
-
Structural biology: A toolbox for protein design.Nature. 2012 Nov 8;491(7423):204-5. doi: 10.1038/491204a. Nature. 2012. PMID: 23135466 No abstract available.
References
Publication types
MeSH terms
Substances
Associated data
- Actions
- Actions
- Actions
- Actions
- Actions
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

