Collective almost synchronisation in complex networks

Abstract

This work introduces the phenomenon of Collective Almost Synchronisation (CAS), which describes a universal way of how patterns can appear in complex networks for small coupling strengths. The CAS phenomenon appears due to the existence of an approximately constant local mean field and is characterised by having nodes with trajectories evolving around periodic stable orbits. Common notion based on statistical knowledge would lead one to interpret the appearance of a local constant mean field as a consequence of the fact that the behaviour of each node is not correlated to the behaviours of the others. Contrary to this common notion, we show that various well known weaker forms of synchronisation (almost, time-lag, phase synchronisation, and generalised synchronisation) appear as a result of the onset of an almost constant local mean field. If the memory is formed in a brain by minimising the coupling strength among neurons and maximising the number of possible patterns, then the CAS phenomenon is a plausible explanation for it.

Figure 1. Results for a network of coupled maps.

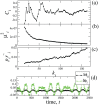
(a) Expected value of the local mean field of the node against the node degree . The error bar indicates the variance () of . (b) A bifurcation diagram of the CAS pattern [Eq. (6)] considering . (c) Probability density function of the trajectory of a node with degree  = 80 (therefore, , ). (d) A return plot considering two nodes ( and ) with the same degree 80.

Figure 2. Results for the Kuramoto network.

Results for . (a) Expected value of the local mean field of a node with degree , picked randomly. Nodes with the same degree present nearly identical local mean fields. (b) The variance of the local mean field. (c) Relationship between the value of and . (d) Phase difference between two nodes, one with degree and the other with degree ; the phase difference between the phases of the trajectory of the node with degree and the phase of its CAS pattern.

Figure 3. Results for a network of Hindmarsh-Rose neurons.

(a) Expected value of the local mean field of the node against the node degree . The error bar indicates the variance () of . (b) Black points indicate the value of and for Eq. (13) to present a stable periodic orbit (no positive Lyapunov exponents). The maximal values of the periodic orbits obtained from Eq. (13) is shown in the bifurcation diagram in (c) considering and . (d) The CAS pattern for a neuron with degree  = 25 (with and ). In the inset, the same CAS pattern of the neuron and some sampled points of the trajectory for the neuron and another neuron with degree . (e) The difference between the first coordinates of the trajectories of neurons and , with a time-lag of . (f) Phase difference between the phases of the trajectories for neurons and .