Measuring decision weights in recognition experiments with multiple response alternatives: comparing the correlation and multinomial-logistic-regression methods

Abstract

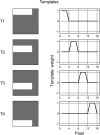
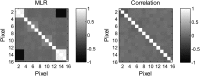
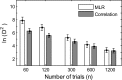
Psychophysical "reverse-correlation" methods allow researchers to gain insight into the perceptual representations and decision weighting strategies of individual subjects in perceptual tasks. Although these methods have gained momentum, until recently their development was limited to experiments involving only two response categories. Recently, two approaches for estimating decision weights in m-alternative experiments have been put forward. One approach extends the two-category correlation method to m > 2 alternatives; the second uses multinomial logistic regression (MLR). In this article, the relative merits of the two methods are discussed, and the issues of convergence and statistical efficiency of the methods are evaluated quantitatively using Monte Carlo simulations. The results indicate that, for a range of values of the number of trials, the estimated weighting patterns are closer to their asymptotic values for the correlation method than for the MLR method. Moreover, for the MLR method, weight estimates for different stimulus components can exhibit strong correlations, making the analysis and interpretation of measured weighting patterns less straightforward than for the correlation method. These and other advantages of the correlation method, which include computational simplicity and a close relationship to other well-established psychophysical reverse-correlation methods, make it an attractive tool to uncover decision strategies in m-alternative experiments.

Figure 1

The four templates used in the virtual-observer simulations. Each row shows one template (from T1 to T4), first (left column) in the form of a matrix represented as a grayscale image [similar to Murray (2011), Fig. 3], then (right column) in the form of a vector represented by a line plot [similar to Dai and Micheyl (2010)]. This illustrates the correspondence between these two types of representations. The vector/line-plot representation is more commonly used in the auditory-perception literature. The matrix/image representation is more commonly used in the visual-perception literature; however, the format can also be used for presenting spectral-temporal weights obtained in auditory perception experiments.

Figure 2

Weighting patterns computed using the multinomial-logistic-regression (MLR) and correlation methods. Weighting patterns computed using Murray's (2011) MLR method are shown in the left-hand column; weighting patterns computed using Dai and Micheyl's (2010) correlation method are shown in the right-hand column. For the latter method, each row shows the weighting pattern corresponding to a particular template (from T1 at the top to T4 at the bottom) shown on the corresponding row of Fig. 1. For the MLR method, the weighting pattern for T4 is flat because the corresponding alternative was used as the reference. The error bars show ±2 SDs of the mean.

Figure 3

Correlation matrices of weighting patterns computed using the MLR (left panel) and correlation methods (right panel). The correspondence between correlation-coefficient values (from −1 to +1) and shades of gray (from black to white) is indicated in the color bar on the right.

Figure 4

Logarithm of the mean Mahalanobis distance squared between weighting patterns based on n trials and “asymptotic” weighting patterns (based on 2000 trials). The error bars show ±1 SDs of the mean. This plot illustrates the convergence of weighting patterns computed using the MLR method (open bars) and the correlation method (closed bars). See the text for additional information concerning the computations underlying this plot.

Figure 5

Weighting patterns for modified templates. The format is the same as that of Fig. 2. (See the text for details.)