Exploring a charge-central strategy in the solution of Poisson's equation for biomolecular applications

Abstract

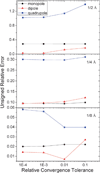
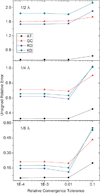
Continuum solvent treatments based on the Poisson-Boltzmann equation have been widely accepted for energetic analysis of biomolecular systems. In these approaches, the molecular solute is treated as a low dielectric region and the solvent is treated as a high dielectric continuum. The existence of a sharp dielectric jump at the solute-solvent interface poses a challenge to model the solvation energetics accurately with such a simple mathematical model. In this study, we explored and evaluated a strategy based on the "induced surface charge" to eliminate the dielectric jump within the finite-difference discretization scheme. In addition to the use of the induced surface charges in solving the equation, the second-order accurate immersed interface method is also incorporated to discretize the equation. The resultant linear system is solved with the GMRES algorithm to explicitly impose the flux conservation condition across the solvent-solute interface. The new strategy was evaluated on both analytical and realistic biomolecular systems. The numerical tests demonstrate the feasibility of utilizing induced surface charge in the finite-difference solution of the Poisson-Boltzmann equation. The analysis data further show that the strategy is consistent with theory and the classical finite-difference method on the tested systems. Limitations of the current implementations and further improvements are also analyzed and discussed to fully bring out its potential of achieving higher numerical accuracy.

Fig. 1

Unsigned relative error (%) of reaction field energies (AUG method) with respect to analytic solutions versus grid spacing (h, Å) for monopole, dipole, and quadrupole respectively. Monopole: a single charge located at (0.5, 0, 0) in a sphere of radius 2 Å, dipole: two charges located at (0, 0, 0.5) and (0, 0, −0.5) respectively, quadrupole: four charges located at (−0.5, −0.5, 0), (0.5, 0.5, 0), (−0.5, 0.5, 0, 0), and (0.5, −0.5, 0) respectively.

Fig. 2

Consistency of reaction field energies (ΔG, kcal mol⁻¹) calculated by the AUG and WHA methods for small molecules. Upper: correlation of the reaction field energies between AUG and WHA at grid spacing 1/8 Å, lower: deviation (%) with respect to energies by the WHA method versus energies by the WHA method. The line in the upper graph is y = x.

Fig. 3

Convergence of reaction field energies (ΔG, kcal mol⁻¹) of the AUG method versus grid spacing (h, Å) on hydrogen-bonding base pairs AT and GC and salt bridging side chain pairs RD and KD, respectively. Solid lines: y = a + bx^c fitting for the AUG method.

Fig. 4

RMS errors of potential (kcal mol⁻¹ Å⁻¹) versus grid spacing (h, Å) with respect to analytical results on the irregular grid points for the WHA and AUG methods of monopole, dipole, and quadrupole, respectively.

Fig. 5

RMS errors of potential (kcal mol⁻¹ Å⁻¹) versus grid spacing (h, Å) with respect to analytical results on the interface for the WHA and AUG methods (upper) and RMS errors of field (kcal mol⁻¹ Å⁻²) on the inner side of the interface (lower) of monopole, dipole, and quadrupole, respectively.

Fig. 6

RMS errors of potential (kcal mol⁻¹ Å⁻¹) versus grid spacing (h, Å) with respect to results calculated at the grid spacing of 1/16 Å on the irregular grid points of AT (upper) and RD (lower), respectively.

Fig. 7

RMS errors of potential (kcal mol⁻¹ Å⁻¹) (upper) and field (kcal mol⁻¹ Å⁻²) (lower) versus grid spacing (h, Å) with respect to results calculated at the grid spacing of 1/16 Å on the inner side of the interface, of AT and RD, respectively.

Fig. 8

Unsigned relative errors (%) of reaction field energies by the AUG method versus relative tolerance for monopole, dipole, and quadrupole, respectively.

Fig. 9

Unsigned relative errors (%) of reaction field energies by the AUG method versus relative tolerance for AT, GC, RD and KD respectively.