Critical closing pressure determined with a model of cerebrovascular impedance

Abstract

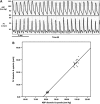
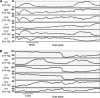
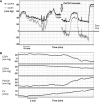
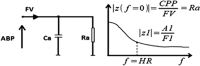
Critical closing pressure (CCP) is the arterial blood pressure (ABP) at which brain vessels collapse and cerebral blood flow (CBF) ceases. Using the concept of impedance to CBF, CCP can be expressed with brain-monitoring parameters: cerebral perfusion pressure (CPP), ABP, blood flow velocity (FV), and heart rate. The novel multiparameter method (CCPm) was compared with traditional transcranial Doppler (TCD) calculations of CCP (CCP1). Digital recordings of ABP, intracranial pressure (ICP), and TCD-based FV from previously published studies of 29 New Zealand White rabbits were reanalyzed. Overall, CCP1 and CCPm showed correlation across wide ranges of ABP, ICP, and PaCO2 (R=0.93, P<0.001). Three physiological perturbations were studied: increase in ICP (n=29) causing both CCP1 and CCPm to increase (P<0.001 for both); reduction of ABP (n=10) resulting in decrease of CCP1 (P=0.006) and CCPm (P=0.002); and controlled increase of PaCO2 (n=8) to hypercapnic levels, which decreased CCP1 and CCPm, albeit insignificantly (P=0.123 and P=0.306 respectively), caused by a spontaneous significant increase in ABP (P=0.025). Multiparameter mathematical model of critical closing pressure explains the relationship of CCP on brain-monitoring variables, allowing the estimation of CCP during cases such as hypercapnia-induced hyperemia, where traditional calculations, like CCP1, often reach negative non-physiological values.

Figure 1

(A) Waveforms of arterial blood pressure (ABP) and flow velocity (FV). (B) Regression line between systolic and diastolic values of ABP and FV. The intercept point between the regression line and the x-axis signifies the pressure at which flow ceases (FV equal to zero) and is equivalent to Burton's critical closing pressure (CCP).

Figure 2

(A) Intracranial hypertension owing to infusion of normal saline into the lumbar subarachnoid space at a rate of 0.15 mL/minute and the corresponding waveforms of arterial blood pressure (ABP), cerebral perfusion pressure (CPP), flow velocity (FV), critical closing pressure (CCP), and wall tension (WT). (B) Trimetaphan induced arterial hypotension and the corresponding waveforms of intracranial pressure (ICP), CPP, FV, CCP, and wall tension (WT). In both figures, CCP has been calculated with the first harmonic model of critical closing pressure (CCP1). Gaps left after artifacts removal have been interpolated graphically.

Figure 3

(A) Correlation between first harmonic model of critical closing pressure (CCP1) and multiparameter mathematical model CCPm. (B) Correlation between first harmonic wall tension model (WT1) and multiparameter mathematical model WTm. (C) Bland–Altman plot for comparing difference between CCPm and CCP1 to average value of CCP1 and CCPm. Note that after the physiological threshold of 40 mm Hg the difference is becoming minimal.

Figure 4

(A) Comparison of first harmonic model of critical closing pressure (CCP1) and multiparameter mathematical model (CCPm) in the maneuver of increase in PaCO₂ (after 13:10). At high PaCO₂, CCP1 decreased to non-physiological negative values, while CCPm stayed positive. (B) Example of gradually increasing PaCO₂ leading to increase of flow velocity (FV), and decrease in both CCP1 and CCPm. Negative values of CCP1 can be seen whereas CCPm stays positive.

Figure 5

(A) Multiparameter mathematical model of wall tension (WTm) is used to demonstrate that wall tension is significantly correlated to cerebrovascular resistance (Ra) (P<0.001) at baseline levels of intracranial pressure (ICP), arterial blood pressure (ABP), and PaCO₂ (normocapnia). (B) Modeled wall tension is significantly correlated to PaCO₂ at baseline ICP and ABP. (C) Relationship between modeled vessel's wall tension and cerebral perfusion pressure cerebral perfusion pressure (CPP) (P=0.001).

Figure 6

Input circuit of electrical model of the cerebrovascular bed and diagram demonstrating the resulting modulus of impedance |z(f)| where f stands for frequency in Hz. Ca, cerebrovascular compliance; Ra, cerebrovascular resistance; CPP, mean cerebral perfusion pressure; FV, mean flow velocity; A1 and F1, first harmonics' amplitudes of arterial blood pressure (ABP) and FV, respectively; HR, frequency (beats/second).