Generalized reproduction numbers and the prediction of patterns in waterborne disease

Abstract

Understanding, predicting, and controlling outbreaks of waterborne diseases are crucial goals of public health policies, but pose challenging problems because infection patterns are influenced by spatial structure and temporal asynchrony. Although explicit spatial modeling is made possible by widespread data mapping of hydrology, transportation infrastructure, population distribution, and sanitation, the precise condition under which a waterborne disease epidemic can start in a spatially explicit setting is still lacking. Here we show that the requirement that all the local reproduction numbers R0 be larger than unity is neither necessary nor sufficient for outbreaks to occur when local settlements are connected by networks of primary and secondary infection mechanisms. To determine onset conditions, we derive general analytical expressions for a reproduction matrix G0, explicitly accounting for spatial distributions of human settlements and pathogen transmission via hydrological and human mobility networks. At disease onset, a generalized reproduction number Λ0 (the dominant eigenvalue of G0) must be larger than unity. We also show that geographical outbreak patterns in complex environments are linked to the dominant eigenvector and to spectral properties of G0. Tests against data and computations for the 2010 Haiti and 2000 KwaZulu-Natal cholera outbreaks, as well as against computations for metapopulation networks, demonstrate that eigenvectors of G0 provide a synthetic and effective tool for predicting the disease course in space and time. Networked connectivity models, describing the interplay between hydrology, epidemiology, and social behavior sustaining human mobility, thus prove to be key tools for emergency management of waterborne infections.

Fig. 1.

Data and model predictions of Haiti epidemic. (A) Total incidence data (weekly cases) from November 2010 to May 2011. (B) Fine-grained spatial distribution of recorded cases cumulated during the onset phase of the epidemic (defined as period from beginning to peak, gray area in A). (C) Comparison of coarse-grained data (department level, labels as in A, Inset) on spatial distributions of cumulated cases (gray bars, onset phase; black bars, whole period) vs. predictions based on the dominant eigenvector (white bars). 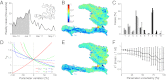= coefficient of determination for the onset phase = 0.81, = coefficient of determination for the whole period = 0.90. (D) Sensitivity to parameter variations of the dominant eigenvalue of G₀. The dotted horizontal line indicates the value below which the disease cannot start. (E) Fine-grained spatial distribution as predicted by dominant eigenvector (SI Text). = 0.92, = 0.95. (F) Sensitivity to parameter variations of correlations between spatial distribution as predicted by dominant eigenvector and actual spatial distribution of cumulated cases (gray, onset phase; black, whole period). Parameter values and details are in SI Text.

Fig. 2.

Data and model predictions of cholera epidemic along the Thukela river network (A, Inset). (A) Total incidence data (weekly cases) from October 2000 to July 2001. Dotted lines mark the model calibration window. (B) Normalized spatial distribution of recorded cases cumulated during the epidemic onset phase (gray in A). (C) Spatial distribution of cases as predicted by the dominant eigenvector. (D) Spatial distribution of local basic reproduction numbers (details in SI Text). Locations in red (blue) are characterized by (). 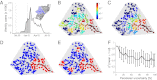(E) Cholera cases (as in B). Red (blue) dots indicate communities with more (less) than 10 reported cases during disease onset. (F) Sensitivity to parameter variations of coefficients of determination and (defined in Fig. 1). Parameter values and additional details are in SI Text.

Fig. 3.

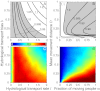
Onset conditions of a waterborne disease epidemic in a Peano network. (A) Effects of hydrological transport parameters for different local reproductive numbers (labels of isolines) in a homogeneous population. Epidemics can start for combinations lying on the left of the curves with , whereas subthreshold epidemics (gray shading) can be triggered for combinations lying in between the relevant isolines. (B) Same as A for human mobility parameters. Epidemics can start for combinations lying on the right of the isolines. (C) As in A, with and Zipf-like population distribution. Different colors code the fraction of realizations (different population distributions) for which onset conditions are met (SI Text). (D) As in C, with reference to mobility parameters. Other parameter values: , , , (A and C), (A and C), (B and D), and (B and D).