A high-performance neural prosthesis enabled by control algorithm design
- PMID: 23160043
- PMCID: PMC3638087
- DOI: 10.1038/nn.3265
A high-performance neural prosthesis enabled by control algorithm design
Abstract
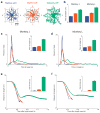
Neural prostheses translate neural activity from the brain into control signals for guiding prosthetic devices, such as computer cursors and robotic limbs, and thus offer individuals with disabilities greater interaction with the world. However, relatively low performance remains a critical barrier to successful clinical translation; current neural prostheses are considerably slower, with less accurate control, than the native arm. Here we present a new control algorithm, the recalibrated feedback intention-trained Kalman filter (ReFIT-KF) that incorporates assumptions about the nature of closed-loop neural prosthetic control. When tested in rhesus monkeys implanted with motor cortical electrode arrays, the ReFIT-KF algorithm outperformed existing neural prosthetic algorithms in all measured domains and halved target acquisition time. This control algorithm permits sustained, uninterrupted use for hours and generalizes to more challenging tasks without retraining. Using this algorithm, we demonstrate repeatable high performance for years after implantation in two monkeys, thereby increasing the clinical viability of neural prostheses.
Conflict of interest statement
The authors declare that they have no competing financial interests.
Figures


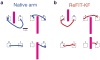
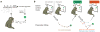
References
-
- Serruya MD, Hatsopoulos NG, Paninski L, Fellows MR, Donoghue JP. Instant neural control of a movement signal. Nature. 2002;416:141–142. - PubMed
-
- Taylor DM, Tillery SI, Schwartz AB. Direct cortical control of 3D neuroprosthetic devices. Science. 2002;296:1829–1832. - PubMed
-
- Velliste M, Perel S, Spalding MC, Whitford AS, Schwartz AB. Cortical control of a prosthetic arm for self-feeding. Nature. 2008;453:1098–1101. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

