A procedure for testing across-condition rhythmic spike-field association change
- PMID: 23164959
- PMCID: PMC3800189
- DOI: 10.1016/j.jneumeth.2012.10.010
A procedure for testing across-condition rhythmic spike-field association change
Abstract
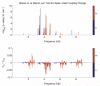
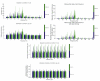
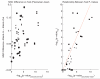
Many experiments in neuroscience have compared the strength of association between neural spike trains and rhythms present in local field potential (LFP) recordings. The measure employed in these comparisons, "spike-field coherence", is a frequency dependent measure of linear association, and is shown to depend on overall neural activity (Lepage et al., 2011). Dependence upon overall neural activity, that is, dependence upon the total number of spikes, renders comparison of spike-field coherence across experimental context difficult. In this paper, an inferential procedure based upon a generalized linear model is shown to be capable of separating the effects of overall neural activity from spike train-LFP oscillatory coupling. This separation provides a means to compare the strength of oscillatory association between spike train-LFP pairs independent of differences in spike counts. Following a review of the generalized linear modelling framework of point process neural activity a specific class of generalized linear models are introduced. This model class, using either a piece-wise constant link function, or an exponential function to relate an LFP rhythm to neural response, is used to develop hypothesis tests capable of detecting changes in spike train-LFP oscillatory coupling. The performance of these tests is validated, both in simulation and on real data. The proposed method of inference provides a principled statistical procedure by which across-context change in spike train-LFP rhythmic association can be directly inferred that explicitly handles between-condition differences in total spike count.
Copyright © 2012 Elsevier B.V. All rights reserved.
Figures

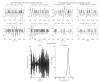


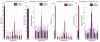
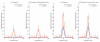
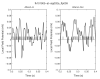





Similar articles
-
Unbiased and robust quantification of synchronization between spikes and local field potential.J Neurosci Methods. 2016 Aug 30;269:33-8. doi: 10.1016/j.jneumeth.2016.05.004. Epub 2016 May 13. J Neurosci Methods. 2016. PMID: 27180930
-
Improved measures of phase-coupling between spikes and the Local Field Potential.J Comput Neurosci. 2012 Aug;33(1):53-75. doi: 10.1007/s10827-011-0374-4. Epub 2011 Dec 21. J Comput Neurosci. 2012. PMID: 22187161 Free PMC article.
-
Single neurons are differently involved in stimulus-specific oscillations in cat visual cortex.Exp Brain Res. 1993;95(1):177-82. doi: 10.1007/BF00229667. Exp Brain Res. 1993. PMID: 8405251
-
Challenges in the quantification and interpretation of spike-LFP relationships.Curr Opin Neurobiol. 2015 Apr;31:111-8. doi: 10.1016/j.conb.2014.09.004. Epub 2014 Oct 3. Curr Opin Neurobiol. 2015. PMID: 25282542 Review.
-
Linking extracellular electric potential in the brain to neural activity - a review of source localization and component identification methods.Acta Neurobiol Exp (Wars). 2015;75(2):117-25. doi: 10.55782/ane-2015-2022. Acta Neurobiol Exp (Wars). 2015. PMID: 26232990 Review.
Cited by
-
Establishing a Statistical Link between Network Oscillations and Neural Synchrony.PLoS Comput Biol. 2015 Oct 14;11(10):e1004549. doi: 10.1371/journal.pcbi.1004549. eCollection 2015 Oct. PLoS Comput Biol. 2015. PMID: 26465621 Free PMC article.
-
Rate-adjusted spike-LFP coherence comparisons from spike-train statistics.J Neurosci Methods. 2015 Jan 30;240:141-53. doi: 10.1016/j.jneumeth.2014.11.012. Epub 2014 Nov 24. J Neurosci Methods. 2015. PMID: 25460189 Free PMC article.
-
Primary sensorimotor cortex exhibits complex dependencies of spike-field coherence on neuronal firing rates, field power, and behavior.J Neurophysiol. 2018 Jul 1;120(1):226-238. doi: 10.1152/jn.00037.2018. Epub 2018 Mar 28. J Neurophysiol. 2018. PMID: 29589815 Free PMC article.
-
Investigating large-scale brain dynamics using field potential recordings: analysis and interpretation.Nat Neurosci. 2018 Jul;21(7):903-919. doi: 10.1038/s41593-018-0171-8. Epub 2018 Jun 25. Nat Neurosci. 2018. PMID: 29942039 Free PMC article. Review.
-
Trigeminal nerve direct current stimulation causes sustained increase in neural activity in the rat hippocampus.Brain Stimul. 2024 May-Jun;17(3):648-659. doi: 10.1016/j.brs.2024.05.005. Epub 2024 May 11. Brain Stimul. 2024. PMID: 38740183 Free PMC article.
References
-
- Akaike H. A new look at the statistical model identification. IEEE Trans Automat Control. 1974;19(6):716–23.
-
- Amjad AM, Halliday DM, Rosenberg JR, Conway BA. An extended difference of coherence test for comparing and combining several independent coherence estimates: theory and application to the study of motor units and physiological tremor. J Neurosci Methods. 1997;73(2/3):69–79. - PubMed
-
- Box GEP, Draper NR. Empirical model-building and response surfaces. Wiley; US, Canada: 1987.
-
- Brillinger DR. The identification of point process systems. Ann Probabil. 1975;3(6):909–24.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

