The dominant folding route minimizes backbone distortion in SH3
- PMID: 23166485
- PMCID: PMC3499259
- DOI: 10.1371/journal.pcbi.1002776
The dominant folding route minimizes backbone distortion in SH3
Abstract
Energetic frustration in protein folding is minimized by evolution to create a smooth and robust energy landscape. As a result the geometry of the native structure provides key constraints that shape protein folding mechanisms. Chain connectivity in particular has been identified as an essential component for realistic behavior of protein folding models. We study the quantitative balance of energetic and geometrical influences on the folding of SH3 in a structure-based model with minimal energetic frustration. A decomposition of the two-dimensional free energy landscape for the folding reaction into relevant energy and entropy contributions reveals that the entropy of the chain is not responsible for the folding mechanism. Instead the preferred folding route through the transition state arises from a cooperative energetic effect. Off-pathway structures are penalized by excess distortion in local backbone configurations and contact pair distances. This energy cost is a new ingredient in the malleable balance of interactions that controls the choice of routes during protein folding.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

 ,
,  and
and  , while the terminal strands
, while the terminal strands  and
and  remain mostly unstructured. Specific packing contacts that are relevant for further folding progress are also present, notably between the RT-loop and
remain mostly unstructured. Specific packing contacts that are relevant for further folding progress are also present, notably between the RT-loop and  . Green and red lines define groups of early- and late-forming hairpin contacts that are chosen to characterise the pattern of formed contacts in individual transition state structures for further analysis.
. Green and red lines define groups of early- and late-forming hairpin contacts that are chosen to characterise the pattern of formed contacts in individual transition state structures for further analysis.
 . C: Entropy contribution
. C: Entropy contribution  . Two dimensional energy landscapes are plotted as a function of the total number of formed contacts
. Two dimensional energy landscapes are plotted as a function of the total number of formed contacts  and of
and of  , which quantifies the pattern of contact formation.
, which quantifies the pattern of contact formation.  is defined such that positive values correspond to a pattern of contact formation in agreement with the dominant folding route, and negative values mean the inverse preference. White triangles in each plot trace the average folding path that corresponds to the WT-dominant mechanism with its polarized transition state structure. The free energy landscape, shown in panel A, has a saddle point between the unfolded and folded basins, located at positive
is defined such that positive values correspond to a pattern of contact formation in agreement with the dominant folding route, and negative values mean the inverse preference. White triangles in each plot trace the average folding path that corresponds to the WT-dominant mechanism with its polarized transition state structure. The free energy landscape, shown in panel A, has a saddle point between the unfolded and folded basins, located at positive  . Off-pathway transitions (negative
. Off-pathway transitions (negative  ) are blocked by a spur of high free energy. The separated energy and entropy contributions are shown in panels B and C. In gray the full free energy landscape is repeated in the background. The energy contribution
) are blocked by a spur of high free energy. The separated energy and entropy contributions are shown in panels B and C. In gray the full free energy landscape is repeated in the background. The energy contribution  , plotted in panel B, shows a peak of high energies at low
, plotted in panel B, shows a peak of high energies at low  in the transition region, which corresponds to the spur blocking off-pathway transitions in
in the transition region, which corresponds to the spur blocking off-pathway transitions in  . In contrast the entropy contribution
. In contrast the entropy contribution  , plotted in panel C, does not show any feature that would favor a polarized transition state structure.
, plotted in panel C, does not show any feature that would favor a polarized transition state structure.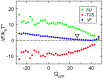
 and the contributions
and the contributions  and
and  in the transition region at
in the transition region at  are plotted as a function of the coordinate
are plotted as a function of the coordinate  , along the dashed line in Fig. 2. Positive values of
, along the dashed line in Fig. 2. Positive values of  correspond to a native-like pattern of contact formation, negative values signal off-pathway structures with a reversed pattern. The white triangle indicates the position of the average WT reaction path. The bias in the free energy
correspond to a native-like pattern of contact formation, negative values signal off-pathway structures with a reversed pattern. The white triangle indicates the position of the average WT reaction path. The bias in the free energy  that is favoring WT-dominant transition states is determined by the consistent slope of the energy contribution
that is favoring WT-dominant transition states is determined by the consistent slope of the energy contribution  . The entropy contribution
. The entropy contribution  shows a weaker opposite slope towards
shows a weaker opposite slope towards  that would penalize the WT-dominant pattern of contact formation.
that would penalize the WT-dominant pattern of contact formation.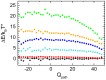
 in dependence on
in dependence on  , in the transition state region at
, in the transition state region at  , is decomposed into the contributions from each term in the structure-based potential. Data are shifted for visibility. From bottom to top the terms shown are: bonds, repulsion, angles, contacts, dihedrals and the total potential energy. The numerically largest parts of the bias towards a WT-dominant pattern of contact formation in the transition state are provided by dihedral angles and contact potentials, followed by angles. The contibution from repulsive interactions is small but significant. Bond stretching interactions are constant along
, is decomposed into the contributions from each term in the structure-based potential. Data are shifted for visibility. From bottom to top the terms shown are: bonds, repulsion, angles, contacts, dihedrals and the total potential energy. The numerically largest parts of the bias towards a WT-dominant pattern of contact formation in the transition state are provided by dihedral angles and contact potentials, followed by angles. The contibution from repulsive interactions is small but significant. Bond stretching interactions are constant along  .
.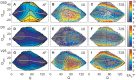
 and of the coordinate
and of the coordinate  that quantifies the pattern of contact formation. Positive values correspond to the pattern in the WT-dominant transition state, negative values mean a reversed pattern. Average folding paths are marked by white triangles. The system D50 retains the WT-dominant pattern of contact formation in its transition state, indicated by positive values of
that quantifies the pattern of contact formation. Positive values correspond to the pattern in the WT-dominant transition state, negative values mean a reversed pattern. Average folding paths are marked by white triangles. The system D50 retains the WT-dominant pattern of contact formation in its transition state, indicated by positive values of  . Both energy and entropy contributions to the landscape follow the same qualitative picture as in the full model. Again, the bias in
. Both energy and entropy contributions to the landscape follow the same qualitative picture as in the full model. Again, the bias in  towards WT-dominant transition states with positive
towards WT-dominant transition states with positive  arises from a peak in the energy contribution at negative
arises from a peak in the energy contribution at negative  , while the entropy contribution provides no such bias. In the system D0 the biasing peak in the energy contribution
, while the entropy contribution provides no such bias. In the system D0 the biasing peak in the energy contribution  is lost. The entropy again provides no bias either. The resulting free energy landscape has a very low broad barrier and leads to an unspecific mechanism. A very similar free energy landscape with low barrier also results for the system V25, which also folds with an unspecific mechanism. Here the biasing feature in the energy contribution
is lost. The entropy again provides no bias either. The resulting free energy landscape has a very low broad barrier and leads to an unspecific mechanism. A very similar free energy landscape with low barrier also results for the system V25, which also folds with an unspecific mechanism. Here the biasing feature in the energy contribution  to the landscape is clearly present, but the entropy contribution
to the landscape is clearly present, but the entropy contribution  is now modified to counteract it.
is now modified to counteract it.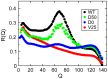
 for the full structure-based model and for the systems D50 and D0 with softer dihedral potentials and V25 with reduced bead size. The peak near
for the full structure-based model and for the systems D50 and D0 with softer dihedral potentials and V25 with reduced bead size. The peak near  for the WT model reflects the specific transition state. In the system D50 with softer dihedral potentials, the transition state is preserved, although with lowered specificity. In the absence of any dihedral potential in the system D0 only very little specificity remains in the transition state. In the system V25 with reduced bead size, the specificity of the transition state is also completely lost and folding takes place on a variety of routes.
for the WT model reflects the specific transition state. In the system D50 with softer dihedral potentials, the transition state is preserved, although with lowered specificity. In the absence of any dihedral potential in the system D0 only very little specificity remains in the transition state. In the system V25 with reduced bead size, the specificity of the transition state is also completely lost and folding takes place on a variety of routes.
 were classified as reversed, neutral or on-pathway according to their mechanistic coordinates of
were classified as reversed, neutral or on-pathway according to their mechanistic coordinates of  ,
,  or
or  , respectively. Averaged structures are shown in panels A–C. Residues with a high average fraction of formed contacts are colored green, regions with strongly distorted dihedral angles are marked in orange. Translucent spheroids give the standard deviations from the average position for residues whose locations vary strongly between configurations. Strong repulsive interactions are marked in red. The underlying data are plotted in the graphs below each structure; with standard deviations of positions in panels D–F, dihedral energies in panels G–I, and the fraction of formed contacts in panels K–M. Horizontal bars indicate the highlighting thresholds. (Figure prepared with VMD .).
, respectively. Averaged structures are shown in panels A–C. Residues with a high average fraction of formed contacts are colored green, regions with strongly distorted dihedral angles are marked in orange. Translucent spheroids give the standard deviations from the average position for residues whose locations vary strongly between configurations. Strong repulsive interactions are marked in red. The underlying data are plotted in the graphs below each structure; with standard deviations of positions in panels D–F, dihedral energies in panels G–I, and the fraction of formed contacts in panels K–M. Horizontal bars indicate the highlighting thresholds. (Figure prepared with VMD .).
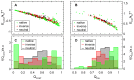
 of structures with the contact formed in panel A, for on-pathway transition states and for both reversed and neutral off-pathway structures. Similarly the average energy from each dihedral is plotted in panel B against the fraction
of structures with the contact formed in panel A, for on-pathway transition states and for both reversed and neutral off-pathway structures. Similarly the average energy from each dihedral is plotted in panel B against the fraction  of structures with the dihedral in its native-like rotamer state, again for on-pathway transition states and for reversed and neutral off-pathway structures. Both contact and dihedral energies naturally decrease with the fraction of native-like local structures. Due to remaining distortions the average stabilization is generally smaller than it would be expected from perfectly native configurations. For frequently formed contacts and dihedrals the downward curvatures of the plots however indicate an added gain in stabilization beyond their increase in frequency. While more rarely formed contacts and dihedrals also remain relatively more distorted even in native-like structures, dihedrals and contacts that are frequently native-like also come closer to their native configuration when they are formed. This relationship appears equally in on-pathway transition states and in off-pathway structures. Histograms of
of structures with the dihedral in its native-like rotamer state, again for on-pathway transition states and for reversed and neutral off-pathway structures. Both contact and dihedral energies naturally decrease with the fraction of native-like local structures. Due to remaining distortions the average stabilization is generally smaller than it would be expected from perfectly native configurations. For frequently formed contacts and dihedrals the downward curvatures of the plots however indicate an added gain in stabilization beyond their increase in frequency. While more rarely formed contacts and dihedrals also remain relatively more distorted even in native-like structures, dihedrals and contacts that are frequently native-like also come closer to their native configuration when they are formed. This relationship appears equally in on-pathway transition states and in off-pathway structures. Histograms of  and
and  shown in panels C and D reveal that on-pathway transition states benefit most from this additional stabilization of frequently native-like contacts and dihedrals, thanks to broadened or even bimodal distributions that maximize the fraction of such very frequently formed contacts and dihedrals.
shown in panels C and D reveal that on-pathway transition states benefit most from this additional stabilization of frequently native-like contacts and dihedrals, thanks to broadened or even bimodal distributions that maximize the fraction of such very frequently formed contacts and dihedrals.Similar articles
-
Balancing energy and entropy: a minimalist model for the characterization of protein folding landscapes.Proc Natl Acad Sci U S A. 2005 Jul 19;102(29):10141-6. doi: 10.1073/pnas.0409471102. Epub 2005 Jul 8. Proc Natl Acad Sci U S A. 2005. PMID: 16006532 Free PMC article.
-
Modeling the interplay between geometrical and energetic effects in protein folding.J Phys Chem B. 2005 Sep 1;109(34):16503-10. doi: 10.1021/jp0512863. J Phys Chem B. 2005. PMID: 16853098
-
Quantitative criteria for native energetic heterogeneity influences in the prediction of protein folding kinetics.Proc Natl Acad Sci U S A. 2009 Jan 13;106(2):434-9. doi: 10.1073/pnas.0810218105. Epub 2008 Dec 15. Proc Natl Acad Sci U S A. 2009. PMID: 19075236 Free PMC article.
-
Fuzziness and Frustration in the Energy Landscape of Protein Folding, Function, and Assembly.Acc Chem Res. 2021 Mar 2;54(5):1251-1259. doi: 10.1021/acs.accounts.0c00813. Epub 2021 Feb 8. Acc Chem Res. 2021. PMID: 33550810 Free PMC article. Review.
-
The folding energy landscape and free energy excitations of cytochrome c.Acc Chem Res. 2010 May 18;43(5):652-60. doi: 10.1021/ar9002703. Acc Chem Res. 2010. PMID: 20143816 Free PMC article. Review.
Cited by
-
Constructing sequence-dependent protein models using coevolutionary information.Protein Sci. 2016 Jan;25(1):111-22. doi: 10.1002/pro.2758. Epub 2015 Aug 10. Protein Sci. 2016. PMID: 26223372 Free PMC article.
-
Structure of the human monomeric NEET protein MiNT and its role in regulating iron and reactive oxygen species in cancer cells.Proc Natl Acad Sci U S A. 2018 Jan 9;115(2):272-277. doi: 10.1073/pnas.1715842115. Epub 2017 Dec 19. Proc Natl Acad Sci U S A. 2018. PMID: 29259115 Free PMC article.
-
Geometrical Frustration in Interleukin-33 Decouples the Dynamics of the Functional Element from the Folding Transition State Ensemble.PLoS One. 2015 Dec 2;10(12):e0144067. doi: 10.1371/journal.pone.0144067. eCollection 2015. PLoS One. 2015. PMID: 26630011 Free PMC article.
-
On Markov blankets and hierarchical self-organisation.J Theor Biol. 2020 Feb 7;486:110089. doi: 10.1016/j.jtbi.2019.110089. Epub 2019 Nov 20. J Theor Biol. 2020. PMID: 31756340 Free PMC article.
-
The Active Inference Approach to Ecological Perception: General Information Dynamics for Natural and Artificial Embodied Cognition.Front Robot AI. 2018 Mar 8;5:21. doi: 10.3389/frobt.2018.00021. eCollection 2018. Front Robot AI. 2018. PMID: 33500908 Free PMC article.
References
-
- Frauenfelder H, Sligar SG, Wolynes PG (1991) The energy landscapes and motions of proteins. Science 254: 1598–1603. - PubMed
-
- Bryngelson JD, Onuchic JN, Socci ND, Wolynes PG (1995) Funnels, pathways, and the energy landscape of protein-folding - a synthesis. Proteins Struct Func Bioinf 21: 167–195. - PubMed
-
- Onuchic JN, Wolynes PG (2004) Theory of protein folding. Curr Opin Struct Biol 14: 70–75. - PubMed
-
- Plotkin S, Onuchic JN (2002) Structural and energetic heterogeneity in protein folding. i. theory. J Chem Phys 116: 5263–5283.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Research Materials

