Variational multiscale models for charge transport
- PMID: 23172978
- PMCID: PMC3501390
- DOI: 10.1137/110845690
Variational multiscale models for charge transport
Abstract
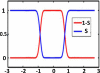
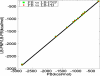
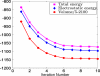
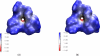
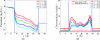
This work presents a few variational multiscale models for charge transport in complex physical, chemical and biological systems and engineering devices, such as fuel cells, solar cells, battery cells, nanofluidics, transistors and ion channels. An essential ingredient of the present models, introduced in an earlier paper (Bulletin of Mathematical Biology, 72, 1562-1622, 2010), is the use of differential geometry theory of surfaces as a natural means to geometrically separate the macroscopic domain from the microscopic domain, meanwhile, dynamically couple discrete and continuum descriptions. Our main strategy is to construct the total energy functional of a charge transport system to encompass the polar and nonpolar free energies of solvation, and chemical potential related energy. By using the Euler-Lagrange variation, coupled Laplace-Beltrami and Poisson-Nernst-Planck (LB-PNP) equations are derived. The solution of the LB-PNP equations leads to the minimization of the total free energy, and explicit profiles of electrostatic potential and densities of charge species. To further reduce the computational complexity, the Boltzmann distribution obtained from the Poisson-Boltzmann (PB) equation is utilized to represent the densities of certain charge species so as to avoid the computationally expensive solution of some Nernst-Planck (NP) equations. Consequently, the coupled Laplace-Beltrami and Poisson-Boltzmann-Nernst-Planck (LB-PBNP) equations are proposed for charge transport in heterogeneous systems. A major emphasis of the present formulation is the consistency between equilibrium LB-PB theory and non-equilibrium LB-PNP theory at equilibrium. Another major emphasis is the capability of the reduced LB-PBNP model to fully recover the prediction of the LB-PNP model at non-equilibrium settings. To account for the fluid impact on the charge transport, we derive coupled Laplace-Beltrami, Poisson-Nernst-Planck and Navier-Stokes equations from the variational principle for chemo-electro-fluid systems. A number of computational algorithms is developed to implement the proposed new variational multiscale models in an efficient manner. A set of ten protein molecules and a realistic ion channel, Gramicidin A, are employed to confirm the consistency and verify the capability. Extensive numerical experiment is designed to validate the proposed variational multiscale models. A good quantitative agreement between our model prediction and the experimental measurement of current-voltage curves is observed for the Gramicidin A channel transport. This paper also provides a brief review of the field.
Figures


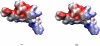
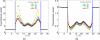
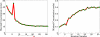
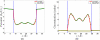


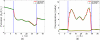

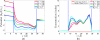

Similar articles
-
Multiscale Multiphysics and Multidomain Models I: Basic Theory.J Theor Comput Chem. 2013 Dec;12(8):10.1142/S021963361341006X. doi: 10.1142/S021963361341006X. J Theor Comput Chem. 2013. PMID: 25382892 Free PMC article.
-
Poisson-Boltzmann-Nernst-Planck model.J Chem Phys. 2011 May 21;134(19):194101. doi: 10.1063/1.3581031. J Chem Phys. 2011. PMID: 21599038 Free PMC article.
-
Quantum dynamics in continuum for proton transport II: Variational solvent-solute interface.Int J Numer Method Biomed Eng. 2012 Jan;28(1):25-51. doi: 10.1002/cnm.1458. Epub 2011 Aug 9. Int J Numer Method Biomed Eng. 2012. PMID: 22328970 Free PMC article.
-
Molecular Mean-Field Theory of Ionic Solutions: A Poisson-Nernst-Planck-Bikerman Model.Entropy (Basel). 2020 May 14;22(5):550. doi: 10.3390/e22050550. Entropy (Basel). 2020. PMID: 33286322 Free PMC article. Review.
-
Development and test of highly accurate endpoint free energy methods. 1: Evaluation of ABCG2 charge model on solvation free energy prediction and optimization of atom radii suitable for more accurate solvation free energy prediction by the PBSA method.J Comput Chem. 2023 May 30;44(14):1334-1346. doi: 10.1002/jcc.27089. Epub 2023 Feb 21. J Comput Chem. 2023. PMID: 36807356 Review.
Cited by
-
Parameter optimization in differential geometry based solvation models.J Chem Phys. 2015 Oct 7;143(13):134119. doi: 10.1063/1.4932342. J Chem Phys. 2015. PMID: 26450304 Free PMC article.
-
Variational approach for nonpolar solvation analysis.J Chem Phys. 2012 Aug 28;137(8):084101. doi: 10.1063/1.4745084. J Chem Phys. 2012. PMID: 22938212 Free PMC article.
-
Competitive Binding of Mg2+ and Na+ Ions to Nucleic Acids: From Helices to Tertiary Structures.Biophys J. 2018 Apr 24;114(8):1776-1790. doi: 10.1016/j.bpj.2018.03.001. Biophys J. 2018. PMID: 29694858 Free PMC article.
-
Persistent homology analysis of protein structure, flexibility, and folding.Int J Numer Method Biomed Eng. 2014 Aug;30(8):814-44. doi: 10.1002/cnm.2655. Epub 2014 Jun 24. Int J Numer Method Biomed Eng. 2014. PMID: 24902720 Free PMC article.
-
Potential of mean force between oppositely charged nanoparticles: A comprehensive comparison between Poisson-Boltzmann theory and Monte Carlo simulations.Sci Rep. 2017 Oct 26;7(1):14145. doi: 10.1038/s41598-017-14636-x. Sci Rep. 2017. PMID: 29074886 Free PMC article.
References
-
- Adalsteinsson H, Debusschere BJ, Long KR, Najm HN. Components for atomisticto-continuum multiscale modeling of flow in micro- and nanofluidic systems. Scient. Program. 2008;16:297–313.
-
- Ahmed SS, Ringhofer C, Vasileska D. Parameter-free effective potential method for use in particle-based device simulations. IEEE Tran. Nanotech. 2008;4:456, 471.
-
- Allen R, Hansen J-P, Melchionna S. Electrostatic potential inside ionic solutions confined by dielectrics: a variational approach. Phys Chem Chem Physics. 2001;3:4177–4186.
-
- Andrei P, Mayergoyz I. Analysis of fluctuations in semiconductor devices through self-consistent Poisson-Schrödinger computations. J. Applied Physics. 2004;96:2071–2079.
-
- Antypov D, Barbosa MC, Holm C. Incorporation of excluded-volume correlations into poisson-boltzmann theory. Physical Review E. 2005;71:061106. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous
