Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2012 Nov 5;20(23):25834-42.
doi: 10.1364/OE.20.025834.

Coupled and uncoupled dipole models of nonlinear scattering

Naveen K Balla  1 , Elijah Y S Yew, Colin J R Sheppard, Peter T C So
Affiliations

Coupled and uncoupled dipole models of nonlinear scattering

Naveen K Balla et al. Opt Express. .

Abstract

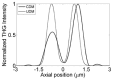
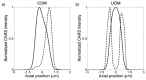
Dipole models are one of the simplest numerical models to understand nonlinear scattering. Existing dipole model for second harmonic generation, third harmonic generation and coherent anti-Stokes Raman scattering assume that the dipoles which make up a scatterer do not interact with one another. Thus, this dipole model can be called the uncoupled dipole model. This dipole model is not sufficient to describe the effects of refractive index of a scatterer or to describe scattering at the edges of a scatterer. Taking into account the interaction between dipoles overcomes these short comings of the uncoupled dipole model. Coupled dipole model has been primarily used for linear scattering studies but it can be extended to predict nonlinear scattering. The coupled and uncoupled dipole models have been compared to highlight their differences. Results of nonlinear scattering predicted by coupled dipole model agree well with previously reported experimental results.

PubMed Disclaimer

Figures

Fig. 1
Fig. 1
Schematic of x-polarized light being focused on a thin layer of actin fibers oriented along x-axis.
Fig. 2
Fig. 2
Distribution of second order polarization component Px(2) induced in a thin layer of actin fiber bundles. Results predicted by UDM (a) and CMD (b&c). Refractive indices of samples (b) and (c) are 1.42 and 1.6 respectively.
Fig. 3
Fig. 3
Distribution of second order polarization components Py(2) (a & c)and Pz(2) (b & d) induced in a thin layer of actin fiber bundles. Results predicted by UDM (a & b) and CMD (c & d). Refractive index of 1.6 was used in CDM calculations.
Fig. 4
Fig. 4
Comparison of forward THG from axial scan of a 1.5 µm polystyrene bead as predicted by UDM and CDM.
Fig. 5
Fig. 5
Comparison of forward (-) and backward (- -) CARS from axial scan of a 1.5 µm polystyrene bead as predicted by a) CDM and b) UDM.
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Gannaway J. N., Sheppard C. J. R., “Second-harmonic imaging in the scanning optical microscope,” Opt. Quantum Electron. 10(5), 435–439 (1978).10.1007/BF00620308 - DOI
    1. Denk W., Strickler J. H., Webb W. W., “Two-photon laser scanning fluorescence microscopy,” Science 248(4951), 73–76 (1990).10.1126/science.2321027 - DOI - PubMed
    1. Campagnola P. J., Wei M. D., Lewis A., Loew L. M., “High-resolution nonlinear optical imaging of live cells by second harmonic generation,” Biophys. J. 77(6), 3341–3349 (1999).10.1016/S0006-3495(99)77165-1 - DOI - PMC - PubMed
    1. Zoumi A., Yeh A., Tromberg B. J., “Imaging cells and extracellular matrix in vivo by using second-harmonic generation and two-photon excited fluorescence,” Proc. Natl. Acad. Sci. U.S.A. 99(17), 11014–11019 (2002).10.1073/pnas.172368799 - DOI - PMC - PubMed
    1. Plotnikov S. V., Millard A. C., Campagnola P. J., Mohler W. A., “Characterization of the myosin-based source for second-harmonic generation from muscle sarcomeres,” Biophys. J. 90(2), 693–703 (2006).10.1529/biophysj.105.071555 - DOI - PMC - PubMed

Publication types