A mathematical model of fluid and gas flow in nanoporous media
- PMID: 23188803
- PMCID: PMC3528606
- DOI: 10.1073/pnas.1219009109
A mathematical model of fluid and gas flow in nanoporous media
Abstract
The mathematical modeling of the flow in nanoporous rocks (e.g., shales) becomes an important new branch of subterranean fluid mechanics. The classic approach that was successfully used in the construction of the technology to develop oil and gas deposits in the United States, Canada, and the Union of Soviet Socialist Republics becomes insufficient for deposits in shales. In the present article a mathematical model of the flow in nanoporous rocks is proposed. The model assumes the rock consists of two components: (i) a matrix, which is more or less an ordinary porous or fissurized-porous medium, and (ii) specific organic inclusions composed of kerogen. These inclusions may have substantial porosity but, due to the nanoscale of pores, tubes, and channels, have extremely low permeability on the order of a nanodarcy (~109-²¹ m² ) or less. These inclusions contain the majority of fluid: oil and gas. Our model is based on the hypothesis that the permeability of the inclusions substantially depends on the pressure gradient. At the beginning of the development of the deposit, boundary layers are formed at the boundaries of the low-permeable inclusions, where the permeability is strongly increased and intensive flow from inclusions to the matrix occurs. The resulting formulae for the production rate of the deposit are presented in explicit form. The formulae demonstrate that the production rate of deposits decays with time following a power law whose exponent lies between -1/2 and -1. Processing of experimental data obtained from various oil and gas deposits in shales demonstrated an instructive agreement with the prediction of the model.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
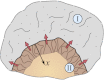
 in the region
in the region  and
and  in the region
in the region  . It is assumed that
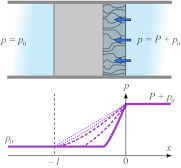
. It is assumed that  , which causes fluid to flow in the negative direction, as shown by the blue arrows. Under the influence of a large pressure gradient, the structure of the filter is deformed and a boundary layer of finite width forms, as shown by the textured blue and gray region. (Lower) Corresponding pressure profile is shown by the solid purple line. The dashed purple lines show the pressure profile at later times as the boundary layer widens to stretch across the width of the filter until it reaches
, which causes fluid to flow in the negative direction, as shown by the blue arrows. Under the influence of a large pressure gradient, the structure of the filter is deformed and a boundary layer of finite width forms, as shown by the textured blue and gray region. (Lower) Corresponding pressure profile is shown by the solid purple line. The dashed purple lines show the pressure profile at later times as the boundary layer widens to stretch across the width of the filter until it reaches  . After this, the stabilization process begins, as shown by the dotted purple lines, and a constant pressure gradient across the filter is achieved eventually.
. After this, the stabilization process begins, as shown by the dotted purple lines, and a constant pressure gradient across the filter is achieved eventually.
 (B) for the nanoporous filtration example, for the case when
(B) for the nanoporous filtration example, for the case when  , for several different values of m. For the cases of
, for several different values of m. For the cases of  , the plots of f have finite support and monotonically decrease until reaching 0 at a finite value of ξ. (A, Inset) Zoomed-in region of one of the curves of f, which has a very small vertical range, demonstrating that the profiles of f are differentiable at the transition.
, the plots of f have finite support and monotonically decrease until reaching 0 at a finite value of ξ. (A, Inset) Zoomed-in region of one of the curves of f, which has a very small vertical range, demonstrating that the profiles of f are differentiable at the transition.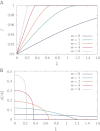
 (B) for the oil extraction problem, for the case of
(B) for the oil extraction problem, for the case of  , for several different values of m.
, for several different values of m.
 for the gas extraction problem for the case of
for the gas extraction problem for the case of  for several different values of m. (B) Profiles of the rescaled permeability show a universality in behavior for different values of m.
for several different values of m. (B) Profiles of the rescaled permeability show a universality in behavior for different values of m.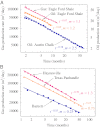
References
-
- US Energy Information Administration . Annual Energy Outlook 2011 with Projections to 2035. Washington, DC: US Department of Energy; 2011. Technical Report.
-
- Silin D, Kneafsey TJ. 2011. Gas shale: From nanometer-scale observations to well modeling (Society of Petroleum Engineers, Richardson, Texas), paper no. 149489.
-
- Tyson RV. Sedimentary Organic Matter: Organic Facies and Palynofacies. London: Chapman & Hall; 1995.
-
- Loucks RG, Reed RM, Ruppel SC, Javie DM. Morphology, genesis, and distribution of nanometer-scale pores in siliceous mudstones of the Mississippian Barnett Shale. J Sediment Res A Sediment Petrol Process. 2009;79:848–861.
-
- Elgmati M, Zobaa M, Zhang H, Bai B, Oboh-Ikuenobe F. 2011. Palynofacies analysis and submicron pore modeling of shale-gas plays (Society of Petroleum Engineers, Richardson, Texas), paper no. 144267.
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

