Optimal multiple surface segmentation with shape and context priors
- PMID: 23193309
- PMCID: PMC4076846
- DOI: 10.1109/TMI.2012.2227120
Optimal multiple surface segmentation with shape and context priors
Abstract
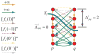
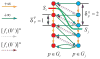
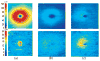
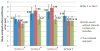
Segmentation of multiple surfaces in medical images is a challenging problem, further complicated by the frequent presence of weak boundary evidence, large object deformations, and mutual influence between adjacent objects. This paper reports a novel approach to multi-object segmentation that incorporates both shape and context prior knowledge in a 3-D graph-theoretic framework to help overcome the stated challenges. We employ an arc-based graph representation to incorporate a wide spectrum of prior information through pair-wise energy terms. In particular, a shape-prior term is used to penalize local shape changes and a context-prior term is used to penalize local surface-distance changes from a model of the expected shape and surface distances, respectively. The globally optimal solution for multiple surfaces is obtained by computing a maximum flow in a low-order polynomial time. The proposed method was validated on intraretinal layer segmentation of optical coherence tomography images and demonstrated statistically significant improvement of segmentation accuracy compared to our earlier graph-search method that was not utilizing shape and context priors. The mean unsigned surface positioning errors obtained by the conventional graph-search approach (6.30 ±1.58 μ m) was improved to 5.14±0.99 μ m when employing our new method with shape and context priors.
Figures




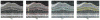
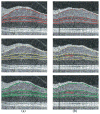

References
-
- Freedman D, Radke R, Zhang T, Jeong Y, Lovelock D, Chen G. Model-based segmentation of medical imagery by matching distributions. IEEE Trans Med Imag. 2005 Mar;24(3):281–292. - PubMed
-
- Vu N, Manjunath B. Shape prior segmentation of multiple objects with graph cuts. Proc. IEEE Int. Conf. Comput. Vis. Pattern Recognit; Jun. 2008,; pp. 1–8.
-
- Wu X, Chen DZ. Optimal net surface problems with applications. Proc. 29th Int. Colloq. Automata, Lang. Programm; 2002; pp. 1029–1042.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

