A method for computing association rate constants of atomistically represented proteins under macromolecular crowding
- PMID: 23197255
- PMCID: PMC3521150
- DOI: 10.1088/1478-3975/9/6/066008
A method for computing association rate constants of atomistically represented proteins under macromolecular crowding
Abstract
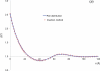
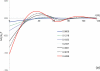
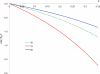
In cellular environments, two protein molecules on their way to form a specific complex encounter many bystander macromolecules. The latter molecules, or crowders, affect both the energetics of the interaction between the test molecules and the dynamics of their relative motion. In earlier work (Zhou and Szabo 1991 J. Chem. Phys. 95 5948-52), it has been shown that, in modeling the association kinetics of the test molecules, the presence of crowders can be accounted for by their energetic and dynamic effects. The recent development of the transient-complex theory for protein association in dilute solutions makes it possible to easily incorporate the energetic and dynamic effects of crowders. The transient complex refers to a late on-pathway intermediate, in which the two protein molecules have near-native relative separation and orientation, but have yet to form the many short-range specific interactions of the native complex. The transient-complex theory predicts the association rate constant as k(a) = k(a0)exp(-ΔG*(el)/k(B)T), where k(a0) is the 'basal' rate constant for reaching the transient complex by unbiased diffusion, and the Boltzmann factors captures the influence of long-range electrostatic interactions between the protein molecules. Crowders slow down the diffusion, therefore reducing the basal rate constant (to k(ac0)), and induce an effective interaction energy ΔG(c). We show that the latter interaction energy for atomistic proteins in the presence of spherical crowders is 'long'-ranged, allowing the association rate constant under crowding to be computed as k(ac) = k(ac0)exp[-(ΔG*(el) + ΔG*(c))/k(B)T]. Applications demonstrate that this computational method allows for realistic modeling of protein association kinetics under crowding.
Figures






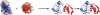


References
-
- Gabdoulline RR, Wade RC. Biomolecular diffusional association. Curr Opin Struc Biol. 2002;12:204–13. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
