Reconstructing mammalian sleep dynamics with data assimilation

Abstract

Data assimilation is a valuable tool in the study of any complex system, where measurements are incomplete, uncertain, or both. It enables the user to take advantage of all available information including experimental measurements and short-term model forecasts of a system. Although data assimilation has been used to study other biological systems, the study of the sleep-wake regulatory network has yet to benefit from this toolset. We present a data assimilation framework based on the unscented Kalman filter (UKF) for combining sparse measurements together with a relatively high-dimensional nonlinear computational model to estimate the state of a model of the sleep-wake regulatory system. We demonstrate with simulation studies that a few noisy variables can be used to accurately reconstruct the remaining hidden variables. We introduce a metric for ranking relative partial observability of computational models, within the UKF framework, that allows us to choose the optimal variables for measurement and also provides a methodology for optimizing framework parameters such as UKF covariance inflation. In addition, we demonstrate a parameter estimation method that allows us to track non-stationary model parameters and accommodate slow dynamics not included in the UKF filter model. Finally, we show that we can even use observed discretized sleep-state, which is not one of the model variables, to reconstruct model state and estimate unknown parameters. Sleep is implicated in many neurological disorders from epilepsy to schizophrenia, but simultaneous observation of the many brain components that regulate this behavior is difficult. We anticipate that this data assimilation framework will enable better understanding of the detailed interactions governing sleep and wake behavior and provide for better, more targeted, therapies.

Figure 1. Computational models of the sleep-wake regulatory system and their outputs.

A) Diniz Behn and Booth (DB) Model circuit diagram, illustrating the cell groups, their output neurotransmitters, and connections. Inhibitory connections are represented by minus and excitatory connections are represented by plus signs. Locus coeruleus (LC), dorsal raphe (DR), ventrolateral preoptic nucleus (VLPO), laterodorsal/pendunculopontine tegmentum (LDT/PPT), gamma-aminobutyric acid (GABA), seretonin (5-HT), norepinephrine (NE), acetylcholine (ACh), homeostatic sleep-drive (h), non rapid-eye-movement sleep (NREM), rapid-eye-movement sleep (REM). B) Typical output of the DB model for three of the cell group firing rates, plus the scored sleep-state plotted as a hypnogram. C) Fleshner, Booth, Forger and Diniz Behn (FBFD) Model circuit diagram, which expands on the DB model to include circadian modulation by and feedback to the suprachiasmatic nucleus (SCN), and allows for diurnal variations in behavior with light periods dominated by sleep activities and dark periods by periods of extended awake activity. Dashed lines indicate SCN additions to DB model. D) 36 hour hypnogram from the FBFD model, with 24-hour periodic CIRC input input to the SCN superimposed.

Figure 2. Reconstruction of DB Model Dynamics (A) with default values for covariance inflater , and (B) after optimization of and .

Noisy measurements of (blue) were passed to the unscented kalman filter (UKF) framework to track and reconstruct all other variables. Shown are the firing rates for the Wake-active (LC), NREM-active (VLPO), and REM-active (LDT/PPT) cell groups, along with thalamic noise . The framework was given the same parameters used to generate the original data. In both A and B the same data was tracked with model initial conditions chosen randomly. After a transient period, reconstructed (red) Wake and NREM dynamics are close to true (black) dynamics. Without optimization the dynamics of are essentially ignored. After optimization at least some of the stochastic dynamics - those that measurably affect the dynamics of - are reconstructed and reconstruction of REM dynamics is improved.

Figure 3. Empirical Observability Coefficient (EOC) matrix.

for the DB model with no thalamic noise and default values of . is an empirical measure of how well variable is reconstructed from measurement of variable . with perfect reconstruction being 1. Here was computed using 12 hours of data. From the matrix, we observe that (row) is poorly observed - poorly reconstructed - from most variables, although its measurement (column) yields good reconstruction of almost all other variables.

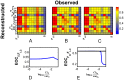
Figure 4. Optimization of Covariance Inflater .

Although the individual EOCs are metrics of reconstruction fidelity, the ranked observability, from the full can be used to guide optimization of the covariance inflater : Poorly observed variables across their rows - low - should have decreased . Variables whose measurement yields poor reconstruction columnwise- low - should have increased . Algorithmically, we iteratively adjust for the variable with the overall lowest mean row or column. In A–C are shown the matrix after each optimization iteration for the full DB model with thalamic noise. A) computed with default values for , i.e. . Note that the lowest mean row/column corresponds to the measurement of , therefore we optimize first. B) after optimization of . C) after optimizing . Shown are as a function of D) for optimization step between A and B and E) for optimization steps between B and C. Optimal values of are chosen from the peaks of these plots.

Figure 5. Parameter estimation with multiple shooting method for reconstruction of DB model from measurement of and with unknown value for parameter .

Parameter estimation is performed by minimizing the divergence between the UKF reconstructed dynamics and short model-generated trajectories that originate on the reconstructed trajectories. To sample the full state space, each step of this minimization averages this divergence over time windows longer than the cycle time of the dynamics. Here we use half hour windows, with 80% overlap. A) Convergence of the estimated parameter to the true value. B) Trajectories for the short model generated (magenta), reconstructed (red), and true (black) dynamics for different periods of the convergence of . Note that initially, for significantly different than the true value, the short trajectories diverge quickly from the reconstructed values, and the reconstructed values of of are different from the true values. When approaches the true value, both short model-generated and reconstructed trajectories approach the true values. C) Reconstruction metric computed for each data assimilation window for three of the variables. As a reference point, the reconstruction metric for the original noisy observation of is shown in blue. Note that although the parameter estimation essentially optimizes short model generated forecasts, it has the effect of optimizing hidden variable reconstruction.

Figure 6. Parameter Tracking to accommodate circadian dynamics.

Noisy measurements of and from the full FBFD model were assimilated with a version of the DB model that represented input from the SCN as a quasi-static parameter whose value was estimated and tracked in 80% overlapping half hour windows. SCN activity imposes circadian and light-driven dynamics that modulate sleep-wake cycles and prevalence of either sleep or wake activity. A) Short excerpts of reconstructed dynamics for various phases of the circadian cycle. B) Estimated (magenta) and true (black) value of the tracked parameter . Note that the tracked value is an estimate, with inherent smoothing on the time scale of a half hour, and therefore does not reconstruct all of the detailed dynamics of the true value which oscillates due to the interplay between the core sleep-wake regulatory cell groups and the SCN. C) Normalized reconstruction error for various variables. As a reference, the reconstruction error for the noisy measurement is shown in blue. The reconstruction of unobserved variables and homeostatic sleep drive is quite good as indicated by small values.

Figure 7. Reconstruction of DB dynamics from measured hypnogram.

SOV is used along with an inferred observation function to translate an observed hypnogram into state conditioned observations for , , and , and their variances. We use the UKF to reconstruct the full variable state space from these observations. A) Probability distributions of firing rates for , and during Wake (black), NREM (red), and REM (blue). These firing rates were generated from the filter-model. B) Hypnogram of observed SOV for a 1 hour time series, with colors to match (A). C) Reconstructed (red) and true (black) traces for , , , and . The inferred observation for is also shown (blue). After a transient period, the reconstruction converges to the true value, even for the homeostatic drive variable which was not observed. However, details of the dynamics that are not accounted for by the state-of-vigilance (SOV) such as brief awakenings and transitions into and out of NREM are not reconstructed well.

Figure 8. Parameter estimation from observed hypnogram for reconstruction of DB model from inferred measurement of , , and with unknown value for parameter .

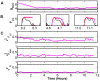
A) Convergence of the estimated parameter(magenta) to the true value (black). B) Trajectories for the short model-generated (magenta), reconstructed (red), and true (black) dynamics for different periods of the convergence of . C) Reconstruction metric computed for each data assimilation window for three of the variables. Horizontal dashed lines correspond to computed from the state-conditioned discrete map used to translate the SOV to model space. Note that once the parameter is optimized, the UKF reconstruction far outperforms the observation map.