Full dynamics of a red blood cell in shear flow
- PMID: 23213229
- PMCID: PMC3529085
- DOI: 10.1073/pnas.1210236109
Full dynamics of a red blood cell in shear flow
Abstract
At the cellular scale, blood fluidity and mass transport depend on the dynamics of red blood cells in blood flow, specifically on their deformation and orientation. These dynamics are governed by cellular rheological properties, such as internal viscosity and cytoskeleton elasticity. In diseases in which cell rheology is altered genetically or by parasitic invasion or by changes in the microenvironment, blood flow may be severely impaired. The nonlinear interplay between cell rheology and flow may generate complex dynamics, which remain largely unexplored experimentally. Under simple shear flow, only two motions, "tumbling" and "tank-treading," have been described experimentally and relate to cell mechanics. Here, we elucidate the full dynamics of red blood cells in shear flow by coupling two videomicroscopy approaches providing multidirectional pictures of cells, and we analyze the mechanical origin of the observed dynamics. We show that contrary to common belief, when red blood cells flip into the flow, their orientation is determined by the shear rate. We discuss the "rolling" motion, similar to a rolling wheel. This motion, which permits the cells to avoid energetically costly deformations, is a true signature of the cytoskeleton elasticity. We highlight a hysteresis cycle and two transient dynamics driven by the shear rate: an intermittent regime during the "tank-treading-to-flipping" transition and a Frisbee-like "spinning" regime during the "rolling-to-tank-treading" transition. Finally, we reveal that the biconcave red cell shape is highly stable under moderate shear stresses, and we interpret this result in terms of stress-free shape and elastic buckling.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

 , time sequence of 10.6 s. (Scale bar, 10 μm.) (B, 2)
, time sequence of 10.6 s. (Scale bar, 10 μm.) (B, 2)  , time sequence of 3.72 s. (B, 3)
, time sequence of 3.72 s. (B, 3)  , time sequence of 3.84 s. (C) Flipping of a hardened RBC at
, time sequence of 3.84 s. (C) Flipping of a hardened RBC at  , time sequence of 1.2 s (DIC image). (D) Temporal increase and stabilization of the angle φ when the shear rate is increased by step, observed on two RBCs (blue and red symbols, respectively) in dextran solution (105 g/mol, c = 9% (wt/wt)). The horizontal bars are the limit value of φ reached for a given shear rate. (D, Inset) Perturbation and recovery of the axis of revolution of an RBC.
, time sequence of 1.2 s (DIC image). (D) Temporal increase and stabilization of the angle φ when the shear rate is increased by step, observed on two RBCs (blue and red symbols, respectively) in dextran solution (105 g/mol, c = 9% (wt/wt)). The horizontal bars are the limit value of φ reached for a given shear rate. (D, Inset) Perturbation and recovery of the axis of revolution of an RBC.  .
.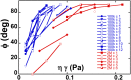
 . Each symbol refers to a single cell suspended in solution [9% (wt/wt)] of dextran of molecular weight 105 g/mol (blue) or 2 106 g/mol (red).
. Each symbol refers to a single cell suspended in solution [9% (wt/wt)] of dextran of molecular weight 105 g/mol (blue) or 2 106 g/mol (red).
 = 9 s−1) and fit by the function
= 9 s−1) and fit by the function  (solid curve). (B) Variation of the orbit of one flipping RBC with increasing shear rate [dextran 2 106 g/mol, c = 9% (wt/wt)]. (B, 1)
(solid curve). (B) Variation of the orbit of one flipping RBC with increasing shear rate [dextran 2 106 g/mol, c = 9% (wt/wt)]. (B, 1)  , time sequence of 10.6 s. (B, 2)
, time sequence of 10.6 s. (B, 2)  , time sequence of 13.72 s. (B, 3)
, time sequence of 13.72 s. (B, 3)  , time sequence of 3.84 s. (C) Variation of the product
, time sequence of 3.84 s. (C) Variation of the product  with the shear rate, where A and B are determined from the fit:
with the shear rate, where A and B are determined from the fit:  . The variation is in agreement with Jeffery and KS laws (solid line: bisector). (C, Inset) Histogram of values of A obtained by the fits for RBCs in various conditions. Stiffened and normal cells in dextran 105 g/mol, c = 9% (wt/wt) (green)
. The variation is in agreement with Jeffery and KS laws (solid line: bisector). (C, Inset) Histogram of values of A obtained by the fits for RBCs in various conditions. Stiffened and normal cells in dextran 105 g/mol, c = 9% (wt/wt) (green)  , (blue)
, (blue)  . Cells in dextran 2 106 g/mol, c = 9% and 7.5%: (green)
. Cells in dextran 2 106 g/mol, c = 9% and 7.5%: (green)  , (blue)
, (blue)  .
.
 , time sequence of 5.48 s. (B) Intermittency at the transition. Sequences show TT, F, and TT, respectively;
, time sequence of 5.48 s. (B) Intermittency at the transition. Sequences show TT, F, and TT, respectively;  ; time sequence of 47.84 s. Tank-treading is detected from the rotation of the bead. The cell is still biconcave with the presence of the dimple (phase contrast image). (C) Transient intermittency. Dotted lines separate tank-treading from flipping regimes. ●, Variation of the bead position between −90° (1st image) to +90° (10th image) vs. time during the tank-treading–flipping transition at
; time sequence of 47.84 s. Tank-treading is detected from the rotation of the bead. The cell is still biconcave with the presence of the dimple (phase contrast image). (C) Transient intermittency. Dotted lines separate tank-treading from flipping regimes. ●, Variation of the bead position between −90° (1st image) to +90° (10th image) vs. time during the tank-treading–flipping transition at  . ♦, Values of the angle φ during the flipping; when φ reaches 40°, the flipping regime is stabilized.
. ♦, Values of the angle φ during the flipping; when φ reaches 40°, the flipping regime is stabilized.
 = 6 s−1, time sequence of 1.98 s.
= 6 s−1, time sequence of 1.98 s.Similar articles
-
Elastic behavior of a red blood cell with the membrane's nonuniform natural state: equilibrium shape, motion transition under shear flow, and elongation during tank-treading motion.Biomech Model Mechanobiol. 2014 Aug;13(4):735-46. doi: 10.1007/s10237-013-0530-z. Epub 2013 Oct 9. Biomech Model Mechanobiol. 2014. PMID: 24104211
-
Red blood cells and other nonspherical capsules in shear flow: oscillatory dynamics and the tank-treading-to-tumbling transition.Phys Rev Lett. 2007 Feb 16;98(7):078301. doi: 10.1103/PhysRevLett.98.078301. Epub 2007 Feb 13. Phys Rev Lett. 2007. PMID: 17359066
-
Dynamics of a single red blood cell in simple shear flow.Phys Rev E Stat Nonlin Soft Matter Phys. 2015 Oct;92(4):042710. doi: 10.1103/PhysRevE.92.042710. Epub 2015 Oct 20. Phys Rev E Stat Nonlin Soft Matter Phys. 2015. PMID: 26565275
-
Red blood cell: from its mechanics to its motion in shear flow.Int J Lab Hematol. 2014 Jun;36(3):237-43. doi: 10.1111/ijlh.12233. Int J Lab Hematol. 2014. PMID: 24750669 Review.
-
Red blood cell mechanics and capillary blood rheology.Cell Biophys. 1991 Jun;18(3):231-51. doi: 10.1007/BF02989816. Cell Biophys. 1991. PMID: 1726534 Review.
Cited by
-
Mechanical perturbations trigger endothelial nitric oxide synthase activity in human red blood cells.Sci Rep. 2016 Jun 27;6:26935. doi: 10.1038/srep26935. Sci Rep. 2016. PMID: 27345770 Free PMC article.
-
AI based image analysis of red blood cells in oscillating microchannels.RSC Adv. 2023 Sep 28;13(41):28576-28582. doi: 10.1039/d3ra04644c. eCollection 2023 Sep 26. RSC Adv. 2023. PMID: 37780736 Free PMC article.
-
A cell-resolved, Lagrangian solver for modeling red blood cell dynamics in macroscale flows.J Comput Phys. 2022 Jul 15;461:111204. doi: 10.1016/j.jcp.2022.111204. Epub 2022 Apr 8. J Comput Phys. 2022. PMID: 36275186 Free PMC article.
-
Microscale flow propulsion through bioinspired and magnetically actuated artificial cilia.Biomicrofluidics. 2015 May 22;9(3):034105. doi: 10.1063/1.4921427. eCollection 2015 May. Biomicrofluidics. 2015. PMID: 26045730 Free PMC article.
-
Separation of spermatozoa from erythrocytes using their tumbling mechanism in a pinch flow fractionation device.Microsyst Nanoeng. 2019 May 20;5:24. doi: 10.1038/s41378-019-0068-z. eCollection 2019. Microsyst Nanoeng. 2019. PMID: 31123596 Free PMC article.
References
-
- Fischer TM, Stöhr-Lissen M, Schmid-Schönbein H. The red cell as a fluid droplet: Tank tread-like motion of the human erythrocyte membrane in shear flow. Science. 1978;202(4370):894–896. - PubMed
-
- Dintenfass L. Internal viscosity of the red cell and a blood viscosity equation. Nature. 1968;219(5157):956–958. - PubMed
-
- Baskurt OK, Meiselman HJ. Blood rheology and hemodynamics. Semin Thromb Hemost. 2003;29(5):435–450. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

