Transition paths, diffusive processes, and preequilibria of protein folding
- PMID: 23213246
- PMCID: PMC3529084
- DOI: 10.1073/pnas.1209891109
Transition paths, diffusive processes, and preequilibria of protein folding
Abstract
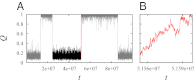
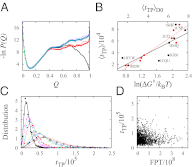
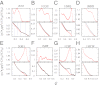
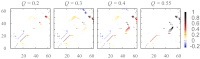
Fundamental relationships between the thermodynamics and kinetics of protein folding were investigated using chain models of natural proteins with diverse folding rates by extensive comparisons between the distribution of conformations in thermodynamic equilibrium and the distribution of conformations sampled along folding trajectories. Consistent with theory and single-molecule experiment, duration of the folding transition paths exhibits only a weak correlation with overall folding time. Conformational distributions of folding trajectories near the overall thermodynamic folding/unfolding barrier show significant deviations from preequilibrium. These deviations, the distribution of transition path times, and the variation of mean transition path time for different proteins can all be rationalized by a diffusive process that we modeled using simple Monte Carlo algorithms with an effective coordinate-independent diffusion coefficient. Conformations in the initial stages of transition paths tend to form more nonlocal contacts than typical conformations with the same number of native contacts. This statistical bias, which is indicative of preferred folding pathways, should be amenable to future single-molecule measurements. We found that the preexponential factor defined in the transition state theory of folding varies from protein to protein and that this variation can be rationalized by our Monte Carlo diffusion model. Thus, protein folding physics is different in certain fundamental respects from the physics envisioned by a simple transition-state picture. Nonetheless, transition state theory can be a useful approximate predictor of cooperative folding speed, because the height of the overall folding barrier is apparently a proxy for related rate-determining physical properties.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
Similar articles
-
Configuration-dependent diffusion can shift the kinetic transition state and barrier height of protein folding.Proc Natl Acad Sci U S A. 2007 Sep 11;104(37):14646-51. doi: 10.1073/pnas.0606506104. Epub 2007 Sep 5. Proc Natl Acad Sci U S A. 2007. PMID: 17804812 Free PMC article.
-
Constrained proper sampling of conformations of transition state ensemble of protein folding.J Chem Phys. 2011 Feb 21;134(7):075103. doi: 10.1063/1.3519056. J Chem Phys. 2011. PMID: 21341875 Free PMC article.
-
Towards a consistent modeling of protein thermodynamic and kinetic cooperativity: how applicable is the transition state picture to folding and unfolding?J Mol Biol. 2002 Jan 25;315(4):899-909. doi: 10.1006/jmbi.2001.5266. J Mol Biol. 2002. PMID: 11812156
-
Coordinate and time-dependent diffusion dynamics in protein folding.Methods. 2010 Sep;52(1):91-8. doi: 10.1016/j.ymeth.2010.04.016. Epub 2010 May 11. Methods. 2010. PMID: 20438841 Review.
-
Probing microscopic conformational dynamics in folding reactions by measuring transition paths.Curr Opin Chem Biol. 2019 Dec;53:68-74. doi: 10.1016/j.cbpa.2019.07.006. Epub 2019 Aug 31. Curr Opin Chem Biol. 2019. PMID: 31479831 Review.
Cited by
-
First passage, looping, and direct transition in expanding and narrowing tubes: Effects of the entropy potential.J Chem Phys. 2017 Oct 7;147(13):134104. doi: 10.1063/1.4993129. J Chem Phys. 2017. PMID: 28987083 Free PMC article.
-
Accelerating Kinetics with Time-Reversal Path Sampling.Molecules. 2023 Dec 18;28(24):8147. doi: 10.3390/molecules28248147. Molecules. 2023. PMID: 38138635 Free PMC article.
-
Understanding biochemical processes in the presence of sub-diffusive behavior of biomolecules in solution and living cells.Biophys Rev. 2019 Dec;11(6):851-872. doi: 10.1007/s12551-019-00580-9. Epub 2019 Aug 23. Biophys Rev. 2019. PMID: 31444739 Free PMC article. Review.
-
Effect of interactions with the chaperonin cavity on protein folding and misfolding.Phys Chem Chem Phys. 2014 Apr 14;16(14):6358-66. doi: 10.1039/c3cp52872c. Epub 2013 Sep 27. Phys Chem Chem Phys. 2014. PMID: 24077053 Free PMC article.
-
Native contact density and nonnative hydrophobic effects in the folding of bacterial immunity proteins.PLoS Comput Biol. 2015 May 27;11(5):e1004260. doi: 10.1371/journal.pcbi.1004260. eCollection 2015 May. PLoS Comput Biol. 2015. PMID: 26016652 Free PMC article.
References
-
- Ikai A, Tanford C. Kinetic evidence for incorrectly folded intermediate states in the refolding of denatured proteins. Nature. 1971;230(5289):100–102. - PubMed
-
- Eyring H. The activated complex in chemical reactions. J Chem Phys. 1935;3:107–115.
-
- Matthews CR. Effect of point mutations on the folding of globular proteins. Methods Enzymol. 1987;154:498–511. - PubMed
-
- Fersht AR, Matouschek A, Serrano L. The folding of an enzyme. I. Theory of protein engineering analysis of stability and pathway of protein folding. J Mol Biol. 1992;224(3):771–782. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

