Design requirements for interfering particles to maintain coadaptive stability with HIV-1

Abstract

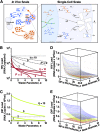
Defective interfering particles (DIPs) are viral deletion mutants lacking essential transacting or packaging elements and must be complemented by wild-type virus to propagate. DIPs transmit through human populations, replicating at the expense of the wild-type virus and acting as molecular parasites of viruses. Consequently, engineered DIPs have been proposed as therapies for a number of diseases, including human immunodeficiency virus (HIV). However, it is not clear if DIP-based therapies would face evolutionary blocks given the high mutation rates and high within-host diversity of lentiviruses. Divergent evolution of HIV and DIPs appears likely since natural DIPs have not been detected for lentiviruses, despite extensive sequencing of HIVs and simian immunodeficiency viruses (SIVs). Here, we tested if the apparent lack of lentiviral DIPs is due to natural selection and analyzed which molecular characteristics a DIP or DIP-based therapy would need to maintain coadaptive stability with HIV-1. Using a well-established mathematical model of HIV-1 in a host extended to include its replication in a single cell and interference from DIP, we calculated evolutionary selection coefficients. The analysis predicts that interference by codimerization between DIPs and HIV-1 genomes is evolutionarily unstable, indicating that recombination between DIPs and HIV-1 would be selected against. In contrast, DIPs that interfere via competition for capsids have the potential to be evolutionarily stable if the capsid-to-genome production ratio of HIV-1 is >1. Thus, HIV-1 variants that attempt to "starve" DIPs to escape interference would be selected against. In summary, the analysis suggests specific experimental measurements that could address the apparent lack of naturally occurring lentiviral DIPs and specifies how therapeutic approaches based on engineered DIPs could be evolutionarily robust and avoid recombination.

Fig 1

Divergent evolution of the HIV-1 and DIP dimerization initiation sequences (DIS) by double mutations in HIV-1 indicates that DIP interference by genome stealing is evolutionarily unstable. (A) Genomic RNA (gRNA) monomers of HIV-1 and a DIP form three types of dimer complexes (HIV-HIV, HIV-DIP, and DIP-DIP) based upon a “kissing-loop” formation between the dimerization initiation sequences of HIV-1 and DIP, which contain a palindromic sequence (e.g., the consensus sequence GCGCGC). Due to a higher rate of transcription and multiple provirus copies, DIP monomers are more abundant, so most HIV-1 RNA is wasted on nonviable HIV-DIP heterodimers. (B) A simplified model representing the abundance of gRNA monomers for HIV-1 and a DIP in the cytoplasm of the infected cell: g(t) and g_DIP(t), respectively. θ is a lumped parameter representing the linear rate of gRNA production, and P is the expression asymmetry between HIV-1 and DIP. k_H, k_DIP, and k_HIP are dimerization coefficients for HIV-HIV, DIP-DIP, and HIV-DIP, respectively. (C) Potential mutations in the kissing loop lead to divergent evolution of HIV-1 and DIP. Top row, in the wild-type (wt) HIV-1 and DIP case, there is an exact match for any gRNA pair (HIV-HIV, HIV-DIP, and DIP-DIP), which is enumerated in the rightmost column. Middle rows, if a single mutation arises within HIV-1 (highlighted by the blue rectangle), HIV-HIV homodimers have two mismatches, whereas HIV-DIP heterodimers have only a single mismatch and DIP-DIP homodimers have no mismatches. Bottom rows, in the (likely) scenario where the second compensatory mutation occurs in HIV, heterodimerization is disfavored compared to homodimerization. (D) Evolutionary fitness of homodimers and heterodimers qualitatively estimated based on dimerization coefficients in panel B and the number of sequence matches in panel C. In this idealized model, fitness takes the canonical functional form of an exponential where the selection coefficient, s, is based only upon the dimerization coefficients and the degree of sequence matching. Although a single mutation in the DIS of HIV-1 is more deleterious to HIV-1 homodimerization than to DIP-to-HIV-1 heterodimerization, a second mutation within the DIS will rescue HIV-1 dimerization and generate a further decrease in DIP-to-HIV-1 genome stealing.

Fig 2

DIPs that steal capsid proteins stably suppress the HIV-1 load across a broad range of parameters. (A) The model comprises two scales of biological organization. The in vivo (individual host) scale is the standard model of HIV-1 replication, expanded to include DIPs (see Supplemental Methods, equations S28 to S33, in the supplemental material). Uninfected cells can be infected with either HIV-1 or DIP, and DIP⁺ cells can be superinfected with HIV-1 to become dually infected cells. The single-cell model is described by equations 1 to 3. A dually infected cell has one integrated HIV-1 provirus and multiple, m, copies of DIP provirus. A fraction of HIV-1 gRNA is translated into proteins that form “empty” capsids. The DIP does not express proteins. Dashed arrows represent multistage processes (including the loss of RNA monomers and capsid proteins). A fraction of stable dimer genomes and full capsids is also lost. Remaining genomes, HIV-1 or the DIP, are packaged within capsids and released as infectious particles. Shown also are the steady-state HIV-1 load (B) and the steady-state DIP load (C) at different values of two single-cell parameters: the capsid waste parameter, κ, and the capsid-to-genome production ratio, η (Table 1). The dashed line indicates the HIV-1 viral load in the absence of capsid waste and the DIP (κ = P = 0), which is assumed to be the average load in untreated humans (3 × 10⁴ RNA copies/ml blood). Calculations use a DIP/HIV-1 production ratio (i.e., expression asymmetry) of P = 5 and a basic reproduction ratio of R₀ = 10 (Table 1). The decrease in HIV-1 load in the presence of capsid waste (κ > 0, red lines), compared to the untreated HIV-1 “set-point” level (dashed line), is partly due to the loss of HIV-1 products (black dotted lines calculated at P = 0) and partly due to the DIP, which competes with HIV-1 for available target cells and steals HIV-1 capsid in dually infected cells. The first effect is more important at η = ∼1, and the DIP suppression factor is stronger at a large η value (see Fig. S2 in the supplemental material). Shown also are the steady-state HIV-1 load (D) and the steady-state DIP load (E) as functions of both expression asymmetry, P, and capsid waste parameter, κ, at three values of the capsid-to-genome ratio: η = 2 (red), η = 5 (green), and η = 10 (blue). These 3D plots act as a partial sensitivity analysis showing that HIV-1 and DIP loads depend strongly on the value of P.

Fig 3

A DIP-HIV interaction is evolutionarily stable over a broad parameter range: HIV-1 cannot escape DIP by decreasing packaging resources. (A) The two-scale model for an individual infected by two strains of HIV, wild type (red) and mutant (orange), as well as a DIP (blue). Mutation causes a small decrease in the packaging constant of both HIV-1 and DIP k_pck and, hence, an increase in capsid waste parameter, κ = αβ/(θk_pck), when ∂κ is >0. (B) Normalized effective selection coefficient, ∂s_eff/(∂κ/κ), for that mutation as a function of κ for a range of capsid-to-genome production ratios η. Fixed parameters are as described for Fig. 2B and C: R₀ = 10 and P = 5. The negative values of ∂s_eff/(∂κ/κ) imply that the mutation has net deleterious effects on HIV-1 replication. Overall, HIV-1 mutations that increase capsid waste are selected against. Inset, HIV-1 load as a function of the waste parameter from Fig. 2B. (C) A negative control showing ∂s_eff/(∂κ/κ) within HIV⁺ DIP⁺ dually infected cells when burst size changes due to increased capsid waste (the first term in equation S54 in the supplemental material) are neglected. Only in this specific context, when burst size changes are ignored, are HIV-1 mutations that increase capsid waste selected for. Shown also are the net ∂s_eff/(∂κ/κ) (D) and control ∂s_eff/(∂κ/κ) (i.e., when burst size changes are neglected) (E) as functions of both P and κ. These 3D plots act as a partial sensitivity analysis and show that the selection coefficient weakly depends on the value of P. Detailed calculations are given in Supplementary Methods in the supplemental material.

Fig 4

DIV-HIV interaction is evolutionarily stable over a broad parameter range: HIV-1 cannot escape a DIP by decreasing the capsid-to-genome ratio. (A) The two-scale model for an individual infected by two strains of HIV-1, wild- type (red) and mutant (orange), as well as a DIP (blue). Mutation causes a small increase in the capsid-to-genome ratio η by ∂η > 0. (B) Normalized effective selection coefficient ∂s_eff/(∂η/η) for that mutation as a function of η for three values of the waste parameter κ. Fixed parameters used are as described for Fig. 2B and C: R₀ = 10 and P = 5. Inset, corresponding HIV-1 viral load as a function of η at three values of the waste parameter κ. The positive values of ∂s_eff/(∂η/η) imply that mutation is selected for, and HIV-1 evolves toward an increasing η value. When κ is 0 and η is <1, the DIP is not dynamically stable in vivo, and the selection coefficient is due exclusively to an increase in the HIV-1 burst size. In a narrow adjacent interval, 1 < η < (P + 1)R₀/[P(R₀ − 1)], DIP is still unstable, and HIV-1 replication does not require more capsid, which is why the selection coefficient is zero. (C) A negative control neglecting HIV-1 burst size changes due to mutation (the first term in equation S54 in the supplemental material) and showing that the effective selection coefficient is positive in the interval where the DIP is stable. The discontinuity at κ = 0 and η = 1 + P is due to DIP gRNA competition with HIV gRNA for capsids at η < 1 + P but not at η > 1 + P, when there are enough capsids for both the DIP and HIV. Shown also are the net ∂s_eff/(∂η/η) (D) and control ∂s_eff/(∂η/η) (E) as functions of both P and η. Discontinuities at η = 1 + mP, m = 1, 2, …, are analogous to the discontinuity described for panel C. These 3D plots act as a partial sensitivity analysis and show that the selection coefficient depends weakly on the value of P.