Spreading out muscle mass within a Hill-type model: a computer simulation study

Abstract

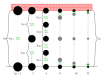
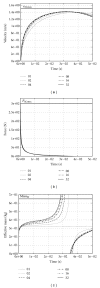
It is state of the art that muscle contraction dynamics is adequately described by a hyperbolic relation between muscle force and contraction velocity (Hill relation), thereby neglecting muscle internal mass inertia (first-order dynamics). Accordingly, the vast majority of modelling approaches also neglect muscle internal inertia. Assuming that such first-order contraction dynamics yet interacts with muscle internal mass distribution, this study investigates two questions: (i) what is the time scale on which the muscle responds to a force step? (ii) How does this response scale with muscle design parameters? Thereto, we simulated accelerated contractions of alternating sequences of Hill-type contractile elements and point masses. We found that in a typical small muscle the force levels off after about 0.2 ms, contraction velocity after about 0.5 ms. In an upscaled version representing bigger mammals' muscles, the force levels off after about 20 ms, and the theoretically expected maximum contraction velocity is not reached. We conclude (i) that it may be indispensable to introduce second-order contributions into muscle models to understand high-frequency muscle responses, particularly in bigger muscles. Additionally, (ii) constructing more elaborate measuring devices seems to be worthwhile to distinguish viscoelastic and inertia properties in rapid contractile responses of muscles.

Figure 1

The six models used for simulating accelerated contractions of a muscle with an overall mass of 6.5 g are arranged from the left to the right. The models differ (i) by having split the muscle mass into an increasing number (I _M + 1) of point masses (PMs; depicted by circles) connected through a corresponding number I _M of CEs (depicted by “brushes”) and (ii) by distributing the optimal muscle length l _M,opt homogeneously to the optimal CE lengths l _CE,opt,i = l _M,opt/I _M. The sum of the circle areas, symbolising the muscle mass, is constant across the six models. The uppermost PM is always fixed to the world, whereas all other PMs can be accelerated by their adjacent CEs. Note that there is no gravity. Generally, l _M = ∑_i=1 ^I_M l _CE,i is the overall muscle length l _M.

Figure 2

Computer simulation of accelerated contractions of six muscle models with the same overall mass (6.5 g), maximum isometric force (30 N), optimal length (0.015 m), and maximum contraction velocity (0.15 m/s). The muscles were fixed at one end and always fully active (q = 1). Models differ just with respect to the number of accelerated discrete point masses approximating a continuous distribution of muscle mass. The point masses were connected by an equal number I _M (see insets in Figure 2) of contractile elements. Their respective optimal lengths l _CE,opt,i were chosen equal to the optimal muscle length l _M,opt divided by I _M. The graph depicts the velocity of the point mass at the free end (a), the force at the fixed end (b), and the effective mass (c), that is, the ratio of force at the fixed end and acceleration of the point mass at the free end, versus time. The effective mass to be expected for an exactly linear acceleration distribution along the muscle would be half of the muscle mass (Mass_M = ℳ; (6): μ _eff = ℳ/2 = 3.25 g). The analytic solution for one CE accelerating one point mass predicts (see Appendix A) a typical time of 3.6 · 10⁻⁴ s for this muscle to approach v _max⁡.

Figure 3

Computer simulation of accelerated contractions of six muscle models with the same overall mass (650 g), maximum isometric force (300 N), optimal length (0.15 m), and maximum contraction velocity (1.5 m/s). The muscles were fixed at one end and always fully active (q = 1). Models differ just with respect to the number of accelerated discrete point masses approximating a continuous distribution of muscle mass. The point masses were connected by an equal number I _M (see insets in Figure 3) of contractile elements. Their respective optimal lengths l _CE,opt,i were chosen equal to the optimal muscle length l _M,opt divided by I _M. The graph depicts velocity (a), force (b), and effective mass (c) versus time. The effective mass to be expected for an exactly linear acceleration distribution along the muscle would be half of the muscle mass (Mass_M = ℳ; (6): μ _eff = ℳ/2 = 325 g). The analytic solution for one CE accelerating one point mass predicts (see Appendix A) a typical time of 3.6 · 10⁻² s for this muscle to approach v _max⁡. Note the hundredfold muscle mass, tenfold maximum isometric force and optimal length, respectively, and hundredfold time scale as compared to the results presented in Figure 2.