Observation of super-resolution in digital breast tomosynthesis

Abstract

Purpose: Digital breast tomosynthesis (DBT) is a 3D x-ray imaging modality in which tomographic sections of the breast are generated from a limited range of tube angles. Because oblique x-ray incidence shifts the image of an object in subpixel detector element increments with each increasing projection angle, it is demonstrated that DBT is capable of super-resolution (i.e., subpixel resolution).

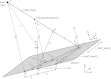
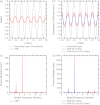
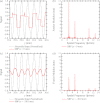
Methods: By convention, DBT reconstructions are performed on planes parallel to the breast support at various depths of the breast volume. In order for resolution in each reconstructed slice to be comparable to the detector, the pixel size should match that of the detector elements; hence, the highest frequency that can be resolved in the plane of reconstruction is the alias frequency of the detector. This study considers reconstruction grids with much smaller pixelation to visualize higher frequencies. For analytical proof of super-resolution, a theoretical framework is developed in which the reconstruction of a high frequency sinusoidal input is calculated using both simple backprojection (SBP) and filtered backprojection. To study the frequency spectrum of the reconstruction, its Fourier transform is also determined. The experimental feasibility of super-resolution was investigated by acquiring images of a bar pattern phantom with frequencies higher than the detector alias frequency.

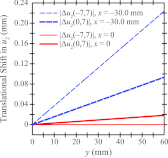
Results: Using analytical modeling, it is shown that the central projection cannot resolve frequencies exceeding the detector alias frequency. The Fourier transform of the central projection is maximized at a lower frequency than the input as evidence of aliasing. By contrast, SBP reconstruction can resolve the input, and its Fourier transform is correctly maximized at the input frequency. Incorporating filters into the reconstruction smoothens pixelation artifacts in the spatial domain and reduces spectral leakage in the Fourier domain. It is also demonstrated that the existence of super-resolution is dependent on position in the reconstruction and on the directionality of the input frequency. Consistent with the analytical results, experimental reconstructions of bar patterns showed visibility of frequencies greater than the detector alias frequency. Super-resolution was present at positions predicted from analytical modeling.

Conclusions: This work demonstrates the existence of super-resolution in DBT. Super-resolution has the potential to impact the visualization of fine structural details in the breast, such as microcalcifications and other subtle signs of cancer.

Figure 1

The 3D input object is a rectangular prism whose linear attenuation coefficient varies sinusoidally with position x parallel to the chest wall side of the breast support. A 2D cross section of the input object through the plane of the chest wall is shown (figure not to scale). In acquiring projection images, the x-ray tube rotates within the xz plane about point B, and the detector simultaneously rotates about the y axis. The primed unit vectors ${\mathbf{i}}_n^{\prime }$ and ${\mathbf{j}}_n^{\prime }$ define the coordinate axes of the plane of the detector for the nth projection.

Figure 2

A schematic diagram of the DBT acquisition geometry is shown (figure not to scale). The x-ray beam strikes point C at the angle θ_n relative to the normal to the detector. In FBP reconstruction, signal at C is backprojected to an arbitrary point E along the incident ray. Within the plane of the detector, backprojection is directed toward point F along the angle Γ_n relative to the ${\mathbf{i}}_n^{\prime }$ axis.

Figure 3

Reconstruction is performed with either the ramp (RA) filter alone or the RA and spectrum apodization (SA) filters together. The SA filter is a Hanning window function.

Figure 4

At a distance u₂ of 30.0 mm from the chest wall, cross sections of detector signal in the central projection (n = 0) and the most oblique projection (n = 7) are plotted versus position u₁. In addition, Fourier transforms are shown versus frequency. The major Fourier peaks do not occur at the input frequency 5.00 lp/mm, illustrating the presence of aliasing. Reducing the source-to-COR distance (h) magnifies the input frequency projected onto the detector.

Figure 5

Unlike a single projection (Fig. 4), simple backprojection (SBP) reconstruction can resolve a high frequency input oriented along the x direction. Applying filters to the reconstruction smoothens pixelation artifacts in the spatial domain and reduces low frequency spectral leakage in the Fourier domain. Reconstructing with the ramp (RA) filter alone has the benefit of greater modulation than reconstructing with the RA and spectrum apodization (SA) filters together. The drawback of reconstructing with the RA filter alone is increasing the amplitude of high frequency spectral leakage.

Figure 6

At a reconstruction depth (z) of 50.0 mm, the magnitude of the translational shift in the u₂ coordinate of the image [Eq. 90] is plotted versus position y measured perpendicular to the chest wall. In the mid PA/SS plane (x = 0), translational shifts are minimal comparing the central projection and an oblique projection (n₁ = 0, n₂ = 7), and are zero comparing the two most oblique projections (n₁ = −7, n₂ = 7). Increasing the magnitude of the distance x relative to the mid PA/SS plane yields a noticeable change in the translational shift.

Figure 7

(a) Within the mid PA/SS plane (x = 0), SBP reconstruction resembles a single projection over the region y ∈ [29.4 mm, 30.6 mm] for an input frequency oriented along the y direction perpendicular to the chest wall. (b) The 1D Fourier transform of the SBP reconstruction is plotted versus frequency measured along the y direction. Within the mid PA/SS plane of a typical sized breast, the major Fourier peak occurs at a frequency lower than the input frequency, 5.00 lp/mm. (c) With x = −30.0 mm, super-resolution in a SBP reconstruction is indeed achievable over the region y ∈ [29.4 mm, 30.6 mm]. (d) For additional proof of super-resolution at x = −30.0 mm, the major peak of the corresponding Fourier transform occurs at the input frequency, 5.00 lp/mm.

Figure 8

For an input frequency oriented along the x direction, the dependency of super-resolution on depth (z₀) is analyzed. The existence of super-resolution is determined from the ratio (r) of the amplitude at the highest peak in the Fourier transform less than the alias frequency of the detector (3.57 lp/mm) to the amplitude at the input frequency (5.00 lp/mm). Super-resolution is present if r < 1 and is absent if r ≥ 1. (a) and (b) Within the mid PA/SS plane (x = 0), super-resolution is not achievable at depths with sharp peaks in the value of r, such as z₀ = 42.2 mm. (c) and (d) By contrast, within the plane x = 60.0 mm, super-resolution is feasible at all depths; r never exceeds unity.

Figure 9

The central projection of a bar pattern phantom misrepresents frequencies higher than the detector alias frequency, 3.57 lp/mm for 140 μm detector elements. For example, at 4.0 lp/mm, Moiré patterns are present. At 5.0 lp/mm, fewer than 30 line pairs are observed over a 6.0 mm length.

Figure 10

Unlike the central projection (Fig. 9), BPF reconstruction can clearly resolve high frequencies along the x direction parallel to the chest wall side of the breast support. Frequencies up to 6.0 lp/mm are resolved with no Moiré patterns or other evidence of aliasing.

Figure 11

Super-resolution along the y direction is analyzed with bar patterns using a BPF reconstruction. The left edges of the even numerals (“4” and “6”) were aligned on the mid PA/SS plane (x = 0), and the separation between 4.0 and 5.0 lp/mm was positioned 30 mm from the chest wall. At the extreme left of the bar patterns, less line pairs are visible than expected, illustrating that super-resolution is not achievable near the plane x = 0. In addition, Moiré patterns at 4.0 lp/mm indicate that super-resolution is not possible too close to the chest wall (y = 0). Super-resolution is evident only at positions sufficiently displaced from the planes x = 0 and y = 0; see the extreme right of the bar patterns at 5.0 and 6.0 lp/mm.

Figure 12

Clinical images of microcalcifications are shown. In (a), BPF reconstruction is performed with pixels matching the detector element size (140 μm), and the result is magnified fourfold to give the image that is shown. In (b), BPF reconstruction is performed using pixels that are much smaller than the detector elements. Image (b) supports super-resolution.