Real-time numerical forecast of global epidemic spreading: case study of 2009 A/H1N1pdm
- PMID: 23237460
- PMCID: PMC3585792
- DOI: 10.1186/1741-7015-10-165
Real-time numerical forecast of global epidemic spreading: case study of 2009 A/H1N1pdm
Abstract
Background: Mathematical and computational models for infectious diseases are increasingly used to support public-health decisions; however, their reliability is currently under debate. Real-time forecasts of epidemic spread using data-driven models have been hindered by the technical challenges posed by parameter estimation and validation. Data gathered for the 2009 H1N1 influenza crisis represent an unprecedented opportunity to validate real-time model predictions and define the main success criteria for different approaches.
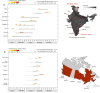
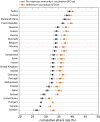
Methods: We used the Global Epidemic and Mobility Model to generate stochastic simulations of epidemic spread worldwide, yielding (among other measures) the incidence and seeding events at a daily resolution for 3,362 subpopulations in 220 countries. Using a Monte Carlo Maximum Likelihood analysis, the model provided an estimate of the seasonal transmission potential during the early phase of the H1N1 pandemic and generated ensemble forecasts for the activity peaks in the northern hemisphere in the fall/winter wave. These results were validated against the real-life surveillance data collected in 48 countries, and their robustness assessed by focusing on 1) the peak timing of the pandemic; 2) the level of spatial resolution allowed by the model; and 3) the clinical attack rate and the effectiveness of the vaccine. In addition, we studied the effect of data incompleteness on the prediction reliability.
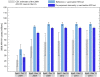
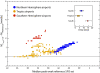
Results: Real-time predictions of the peak timing are found to be in good agreement with the empirical data, showing strong robustness to data that may not be accessible in real time (such as pre-exposure immunity and adherence to vaccination campaigns), but that affect the predictions for the attack rates. The timing and spatial unfolding of the pandemic are critically sensitive to the level of mobility data integrated into the model.
Conclusions: Our results show that large-scale models can be used to provide valuable real-time forecasts of influenza spreading, but they require high-performance computing. The quality of the forecast depends on the level of data integration, thus stressing the need for high-quality data in population-based models, and of progressive updates of validated available empirical knowledge to inform these models.
Figures


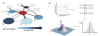




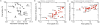



References
-
- Balcan D, Hu H, Gonçalves B, Bajardi P, Poletto C, Ramasco JJ, Paolotti D, Perra N, Tizzoni M, Van den Broeck W, Colizza V, Vespignani A. Seasonal transmission potential and activity peaks of the new influenza A/H1N1: a Monte Carlo likelihood analysis based on human mobility. BMC Med. 2009;7:45. doi: 10.1186/1741-7015-7-45. - DOI - PMC - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

