Non-local statistical label fusion for multi-atlas segmentation

Abstract

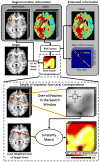
Multi-atlas segmentation provides a general purpose, fully-automated approach for transferring spatial information from an existing dataset ("atlases") to a previously unseen context ("target") through image registration. The method to resolve voxelwise label conflicts between the registered atlases ("label fusion") has a substantial impact on segmentation quality. Ideally, statistical fusion algorithms (e.g., STAPLE) would result in accurate segmentations as they provide a framework to elegantly integrate models of rater performance. The accuracy of statistical fusion hinges upon accurately modeling the underlying process of how raters err. Despite success on human raters, current approaches inaccurately model multi-atlas behavior as they fail to seamlessly incorporate exogenous intensity information into the estimation process. As a result, locally weighted voting algorithms represent the de facto standard fusion approach in clinical applications. Moreover, regardless of the approach, fusion algorithms are generally dependent upon large atlas sets and highly accurate registration as they implicitly assume that the registered atlases form a collectively unbiased representation of the target. Herein, we propose a novel statistical fusion algorithm, Non-Local STAPLE (NLS). NLS reformulates the STAPLE framework from a non-local means perspective in order to learn what label an atlas would have observed, given perfect correspondence. Through this reformulation, NLS (1) seamlessly integrates intensity into the estimation process, (2) provides a theoretically consistent model of multi-atlas observation error, and (3) largely diminishes the need for large atlas sets and very high-quality registrations. We assess the sensitivity and optimality of the approach and demonstrate significant improvement in two empirical multi-atlas experiments.

Fig. 1

Flowchart of the Non-Local STAPLE (NLS) algorithm. NLS integrates a non-local correspondence model (using the atlas-target intensity relationships) into the estimation process. Point-wise correspondence is constructed in a traditional non-local means approach.

Fig. 2

Simulated models of rater behavior and their impact on fusion performance. The first two examples present traditional models of human observation behavior, and, for both models, STAPLE substantially outperforms a majority voting based approach. In contrast, the third example simulates a typical multi-atlas observation model. In this case, STAPLE is outperformed by a majority vote. Additionally, the multi-atlas fusion approaches that utilize the target-atlas intensity relationships (e.g., locally weighted vote and the proposed Non-Local STAPLE) provide substantial improvement.

Fig. 3

Results of the empirical multi-atlas segmentation of the thyroid. The quantitative results (A) show that NLS provides significant improvement in terms of the DSC, Hausdorff distance, and mean surface distance, with a 3 × 3 × 3 patch neighborhood as the most consistent performer. The qualitative results (B) support the quantitative improvement and demonstrate that NLS provides substantial improvement in shape, boundary, and point-wise surface distance error. Note that “Subject Type 1” underwent a surgery to surgically bisect the thyroid.

Fig. 4

Overall accuracy, in terms of mean DSC, comparison for whole-brain segmentation. For both pairwise non-rigid and pairwise affine registration procedures, NLS provides significant improvement over traditional fusion approaches.

Fig. 5

Per-label accuracy comparison on the whole-brain segmentation problem using a pairwise non-rigid registration procedure. NLS provides consistent improvement over locally weighted voting. In this case, NLS using a single voxel patch neighborhood consistently outperformed a larger (3 × 3 × 3) patch neighborhood.

Fig. 6

Per-label accuracy comparison on the whole-brain segmentation problem using a pairwise affine registration procedure. As in Fig. 5, NLS provides consistent improvement over locally weighted voting. In this case, NLS using a larger (3 × 3 × 3) patch neighborhood consistently outperformed a single voxel patch neighborhood.

Fig. 7

Qualitative comparison between the various fusion algorithms for whole-brain segmentation using 5 atlases. For both registration procedures, the qualitative results support the quantitative improvement demonstrated by NLS in Figs. 4–6. The NLS results are qualitatively superior to alternative voting-based procedures in terms of overall shape, size, location and appearance. Note that the mean DSC labels indicate the mean observed DSC for all labels for the corresponding subject (row) and algorithm (column).

Fig. 8

Sensitivity to NLS model parameters. The sensitivity of NLS to σ_i (A) and σ_d (B) demonstrate degraded performance for values that are either too small or too large. Regardless, consistent improvement over a locally weighted vote is achieved. Gray outlines indicate the values used in the previously presented experiments. The qualitative results demonstrate the benefits and detriments of optimal and sub-optimal model parameter values.

Fig. 9

Assessment of the model optimality of the NLS approach. The results using ideal STAPLE and ideal NLS represent the estimates using the globally ideal performance level parameters with 5 atlases per estimate. NLS consistently converged to an estimate that is very close to “ideal” NLS (i.e., the global optimum). On the other hand, STAPLE consistently converged to a value significantly less than the global optimum. Additionally, the results of the “Ideal STAPLE” approach are only slightly better than a MV, which indicates the non-optimality of the traditional STAPLE observation model.

Fig. 10

Comparison to non-local voting fusion. NLS provided consistent improvement over non-local voting, particularly for the smaller deep brain structures (A). NLS provided significant improvement on 18 of the 25 considered labels. Particularly for the smaller labels, the benefits of the proposed multi-atlas rater model are evident. The qualitative comparison (B) supports the per-label comparison and demonstrates the type of improvement achieved by NLS.