A cell-level biomechanical model of Drosophila dorsal closure

Abstract

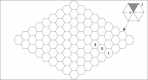
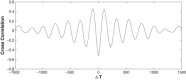
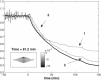
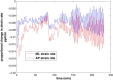
We report a model describing the various stages of dorsal closure of Drosophila. Inspired by experimental observations, we represent the amnioserosa by 81 hexagonal cells that are coupled mechanically through the position of the nodes and the elastic forces on the edges. In addition, each cell has radial spokes representing actin filaments on which myosin motors can attach and exert contractile forces on the nodes, the attachment being controlled by a signaling molecule. Thus, the model couples dissipative cell and tissue motion with kinetic equations describing the myosin and signal dynamics. In the early phase, amnioserosa cells oscillate as a result of coupling among the chemical signaling, myosin attachment/detachment, and mechanical deformation of neighboring cells. In the slow phase, we test two ratcheting mechanisms suggested by experiments: an internal ratchet by the apical and junctional myosin condensates, and an external one by the supracellular actin cables encircling the amnioserosa. Within the range of parameters tested, the model predictions suggest the former as the main contributor to cell and tissue area reduction in this stage. In the fast phase of dorsal closure, cell pulsation is arrested, and the cell and tissue areas contract consistently. This is realized in the model by gradually shrinking the resting length of the spokes. Overall, the model captures the key features of dorsal closure through the three distinct phases, and its predictions are in good agreement with observations.

Figure 1

Model of the AS tissue composed of 81 hexagonal cells. (Inset) Each cell has six edges and six spokes. (Shaded area) Local triangle to the spoke ij.

Figure 2

Early phase: fluctuation of the cell area (thin line) and myosin level (thick line) in cell 3 of Fig. 1. Time t = 0 is set to be the onset of net AS contraction, i.e., the end of the early phase and start of the slow phase.

Figure 3

Distribution of the expansion/contraction time ratio among all cells in the tissue. For most cells, the contraction happens more rapidly than the expansion.

Figure 4

Cross-correlation of the cell area variation among neighbors in the AS tissue. ΔT is the time lag used in computing the cross-correlation, and the negative peak at ΔT = 0 indicates anti-phase oscillation between neighbors.

Figure 5

Rate of area contraction (negative) and expansion (positive) for each cell in the AS tissue. The rate is normalized by the cell area and has unit of s⁻¹, with the grayscale assigned according to the scale bars to the right of each plot. (Top panel) The two snapshots are at (a) t = −39.2 min and (b) −25.2 min. The apparent symmetry in the patterns is due to the initially uniform s and m distributions. (Bottom panel) Asymmetric patterns predicted from nonuniform initial conditions. The two snapshots are at (c) t = −40.5 min and (d) −22.5 min.

Figure 6

Temporal evolutions of the normalized cell area for cells 1 and 2 (see Fig. 1, thin lines) and the normalized tissue area (thick line). The internal ratcheting is modeled by reducing the resting length of the edges and spokes of a cell by 3% in each oscillation cycle. Cells 1 and 2 stop oscillating at ∼t = 50 and 80 min, respectively. (Inset) Snapshot of the tissue at the end of the slow phase, with the grayscale marking the rate of normalized area change in unit of s⁻¹.

Figure 7

AC ratcheting with K = 0.1 nN/μm and δL₀ = 0.01 L₀. (Top panel) Evolution of the normalized tissue area. (Insets) Tissue shape before and after AC ratcheting is activated. (Lower panel) Area oscillation for cells 1 and 2.

Figure 8

Time evolution of the normalized tissue area through the three phases. (Insets) Tissue shape and area contraction rate distribution (in grayscale) at t = 105.2 and 191.8 min. Internal and AC ratchets are both activated at the onset of DC (t = 0). After the start of the fast phase (t = 80 min), the resting length of the cellular segments and the AC cable are reduced at regular periods.

Figure 9

Anisotropic contraction of the AS tissue indicated by the strain rates along the medial-lateral (ML) and anterior-posterior (AP) directions. The ML contraction is twice as strong as the AP contraction, and becomes especially active toward the late stage of DC.