A common optimization principle for motor execution in healthy subjects and parkinsonian patients

Abstract

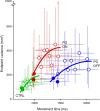
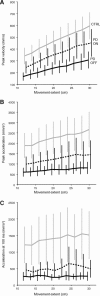
Recent research on Parkinson's disease (PD) has emphasized that parkinsonian movement, although bradykinetic, shares many attributes with healthy behavior. This observation led to the suggestion that bradykinesia in PD could be due to a reduction in motor motivation. This hypothesis can be tested in the framework of optimal control theory, which accounts for many characteristics of healthy human movement while providing a link between the motor behavior and a cost/benefit trade-off. This approach offers the opportunity to interpret movement deficits of PD patients in the light of a computational theory of normal motor control. We studied 14 PD patients with bilateral subthalamic nucleus (STN) stimulation and 16 age-matched healthy controls, and tested whether reaching movements were governed by similar rules in these two groups. A single optimal control model accounted for the reaching movements of healthy subjects and PD patients, whatever the condition of STN stimulation (on or off). The choice of movement speed was explained in all subjects by the existence of a preset dynamic range for the motor signals. This range was idiosyncratic and applied to all movements regardless of their amplitude. In PD patients this dynamic range was abnormally narrow and correlated with bradykinesia. STN stimulation reduced bradykinesia and widened this range in all patients, but did not restore it to a normal value. These results, consistent with the motor motivation hypothesis, suggest that constrained optimization of motor effort is the main determinant of movement planning (choice of speed) and movement production, in both healthy and PD subjects.

Figure 1.

A, Experimental setup. Subjects held the handle and made linear movements toward the targets. Targets were 5 mm diameter LED, seen reflected on a semisilvered mirror. The tip of the handle contained an LED that was extinguished during the movements. This LED appeared 5 mm below the virtual plane of the targets. Handle position was measured by a magnetostrictive device connected to a real-time computer controlling the LEDs. B, Biomechanical model used: a two-link planar arm with four muscles. C, Model structure: transformation from muscle commands to kinematics. In the model, the muscle command minimizes the total neuromuscular cost.

Figure 2.

Mean movement time as a function of movement amplitude for the two groups. Error bars indicate 95% confidence intervals. Solid black: PD patients Off-DBS. Dotted: PD patients On-DBS. Gray: control subjects. For clarity, bars were slightly offset horizontally.

Figure 3.

Median endpoint variance as a function of median movement duration. Filled symbols denote the two smallest amplitudes. Blue: PD patients, Off-DBS. Red: PD patients, On-DBS. Green: control subjects. For each group, a fit corresponding to Fitts' law is figured in bold lines of corresponding color (using a system of two equations, MD = a + b.log(A/W_e) and MD = c + d.A where MD is movement duration, A is movement amplitude, and W_e the SD of endpoints; see Materials and Methods). Error bars indicate the interval between the first and last quartile.

Figure 4.

Kinematic parameters of the movement. Mean peak velocity (A), peak acceleration (B), and initial acceleration 100 ms after movement onset (C), as a function of movement amplitude. Conventions as in Figure 2.

Figure 5.

Results of a minimum-effort model constrained to respect the actual movement durations. The predicted peak velocity (A), peak acceleration (B), time to peak velocity (C), and time to peak acceleration (D) are plotted as a function of the actual data for each PD patient (blue: Off-DBS, red: On-DBS) and control subject (green). Each point corresponds to the median across targets of the median across repetitions to this target. Note the continuum between the results of each group. Dashed line: main diagonal. For clarity, a logarithmic scale was used for B.

Figure 6.

Influence of movement extent on different measures of effort. A, Definition of the motor command range and mean agonist command shown in B and C. Gray lines illustrate motor command signals. B, Motor command range, as derived from the experimental data. Left: PD patients, Off-DBS; middle: PD, On-DBS; right: control subjects. For each experimental trial, the model was constrained to respect actual movement extent and duration. The range is shown averaged across repetitions to the same target and normalized to the median across Off-DBS patients of the mean range for the nearest target (12 cm). Slopes of robust linear fits to the curves were computed for each individual; we indicate the group significance of these slopes. The median across subjects is shown in bold line. C, Average first shoulder agonist command, as in B. D, Total movement work, as in B. For the sake of clarity, the ordinate scale in B and C is logarithmic.

Figure 7.

Illustration of the consequences of a restricted motor range on motor signals (A) and muscle activity (B) for the muscles of the shoulder joint during two movements, one of small amplitude (top row) and one of large amplitude (bottom row). The agonist (solid lines) and antagonist (dashed) signals are represented for an average healthy subject (green) or Off-DBS PD patient (blue). The antagonist trace is inverted for clarity. A, As the neuromuscular effort to reach the target is always minimized, the restriction of motor range translates into longer movement times, for movements of small (top) or large amplitude (bottom). The constraint of the motor range also results in a scaling of movement duration (MD) with movement extent (compare MD for a small and a large amplitude, in both an average healthy and PD subject). B, The restricted motor range leads to lower muscle activities. Nevertheless, peak muscle activity scales with movement amplitude (compare the amplitude of the first agonist burst for a small (top) or large (bottom) movement). This can be observed in both healthy and PD subjects, although it is only clearly visible for the former on these graphs.

Figure 8.

Prediction of the movement duration from the measured motor range, over a wide span of movement amplitudes. The minimum effort model was constrained to respect the motor range of each subject. A, Movement duration as a function of amplitude for six representative subjects, three PD patients On-DBS and Off-DBS, and three control subjects (colored lines, same conventions as in Fig. 6), compared with the prediction derived from their average motor range across targets (gray lines). Brackets indicate the correspondence between the Off-DBS and On-DBS state for each patient. B, Same plot as A, for the group average of movement duration and the prediction derived from the average motor range of each group. Note that due to nonlinearities in the biomechanics, this virtual “mean subject” is not expected to be a perfect fit to the mean behavior. The average upper limit of the motor range was defined as the across-subject geometric mean of limits. Shades of gray identify the group modeled. Light gray, PD Off-DBS; medium gray, PD On-DBS; dark gray, controls. Error bars indicate 95% confidence intervals.

Figure 9.

Effect of STN-DBS on the motor range (A) and relationship between DBS-induced widening of motor range and improvement of the UPDRS restricted to right-hand items (B). A, The motor range when On-DBS was systematically wider than its Off-DBS counterpart, for each patient (circles). Both motor spans were strongly correlated over the population. Bold line, linear regression; dashed line: first diagonal. Note the logarithmic scale on both axes. B, The On/Off ratio of motor ranges was correlated to the reduction of the UPDRS score restricted to right-hand items. Bold line: linear regression. Note the logarithmic scale for ordinates.