On the Dielectric Boundary in Poisson-Boltzmann Calculations

Abstract

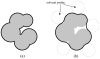
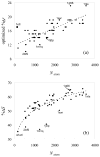
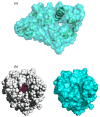
In applying the Poisson-Boltzmann (PB) equation for calculating the electrostatic free energies of solute molecules, an open question is how to specify the boundary between the low-dielectric solute and the high-dielectric solvent. Two common specifications of the dielectric boundary, as the molecular surface (MS) or the van der Waals (vdW) surface of the solute, give very different results for the electrostatic free energy of the solute. With the same atomic radii, the solute is more solvent-exposed in the vdW specification. One way to resolve the difference is to use different sets of atomic radii for the two surfaces. The radii for the vdW surface would be larger in order to compensate for the higher solvent exposure. Here we show that radius re-parameterization required for bringing MS-based and vdW-based PB results to agreement is solute-size dependent. The difference in atomic radii for individual amino acids as solutes is only 2-5% but increases to over 20% for proteins with ~200 residues. Therefore two sets of radii that yield identical MS-based and vdW-based PB results for small solutes will give very different PB results for large solutes. This finding raises issues about two common practices. The first is the use of atomic radii, which are parameterized against either experimental solvation data or data obtained from explicit-solvent simulations on small compounds, for PB calculations on proteins. The second is the parameterization of vdW-based generalized Born models against MS-based PB results.

Figure 1

Definitions of (a) the van der Waals surface and (b) the molecular surface. In this two-dimensional illustration, atoms are represented by gray disks. In (a), the exposed boundaries of the disks, shown in dark, constitute the van der Waals surface. In (b), a spherical solvent probe is rolled around the solute molecule. In addition to the van der Waals spheres, small crevices inaccessible to the solvent probe are now part of the solute region. The boundary of this filled-up solute region, shown in dark, is the molecular surface.

Figure 2

Comparison of the electrostatic solvation energies of the 55 test proteins from MS-based and vdW-based PB calculations. For MS-based PB calculations, the Bondi radii are always used. (a) ΔG_solv^vdW calculated with Bondi radii. (b) ΔG_solv^vdW calculated with atomic radii increased by 6% from the Bondi values.

Figure 3

The percentage increase in atomic radii from the Bondi values required for ΔG_solv^vdW to match with ΔG_solv^MS for 20 types of amino acids as solutes.

Figure 4

(a) The percent increases in atomic radii, %Δr, for optimal agreement between ΔG_solv^vdW and ΔG_solv^MS on the 55 test proteins. (b) Percentage of difference in vdW surface area and MS area, 100(S^vdW – S^MS)/S^vdW, against the number of atom.

Figure 5

Comparison of van der Waals and molecular surfaces. (a) A well-exposed protein, 1m1q, which has the shape of a thin disk. The green ribbon representation of the protein is enclosed by the molecular surface in cyan; a hole appears near the center of the disk shape. (b) A protein, 1g66, with a deep channel. In the left panel, the van der Waals surface is presented, and residues lining the wall of the channel are displayed in red (for the catalytic triad) or purple. In the right panel, the molecular surface is presented. The active site now appears as an indent, but there is no channel penetrating into the center of the protein.

Figure 6

Comparison of actual optimized %Δr values against those predicted from a multi-linear relation.