Quantifying T lymphocyte turnover
- PMID: 23313150
- PMCID: PMC3640348
- DOI: 10.1016/j.jtbi.2012.12.025
Quantifying T lymphocyte turnover
Abstract
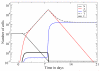
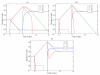
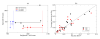
Peripheral T cell populations are maintained by production of naive T cells in the thymus, clonal expansion of activated cells, cellular self-renewal (or homeostatic proliferation), and density dependent cell life spans. A variety of experimental techniques have been employed to quantify the relative contributions of these processes. In modern studies lymphocytes are typically labeled with 5-bromo-2'-deoxyuridine (BrdU), deuterium, or the fluorescent dye carboxy-fluorescein diacetate succinimidyl ester (CFSE), their division history has been studied by monitoring telomere shortening and the dilution of T cell receptor excision circles (TRECs) or the dye CFSE, and clonal expansion has been documented by recording changes in the population densities of antigen specific cells. Proper interpretation of such data in terms of the underlying rates of T cell production, division, and death has proven to be notoriously difficult and involves mathematical modeling. We review the various models that have been developed for each of these techniques, discuss which models seem most appropriate for what type of data, reveal open problems that require better models, and pinpoint how the assumptions underlying a mathematical model may influence the interpretation of data. Elaborating various successful cases where modeling has delivered new insights in T cell population dynamics, this review provides quantitative estimates of several processes involved in the maintenance of naive and memory, CD4(+) and CD8(+) T cell pools in mice and men.
Copyright © 2013 Elsevier Ltd. All rights reserved.
Figures



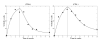
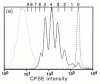
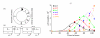
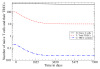
References
-
- Althaus CL, Ganusov VV, De Boer RJ. Dynamics of CD8+ T cell responses during acute and chronic lymphocytic choriomeningitis virus infection. J. Immunol. 2007;179:2944–2951. - PubMed
-
- Antia R, Bergstrom CT, Pilyugin SS, Kaech SM, Ahmed R. Models of CD8+ responses: 1. What is the antigen-independent proliferation program. J. theor. Biol. 2003;221:585–598. - PubMed
-
- Antia R, Ganusov VV, Ahmed R. The role of models in understanding CD8+ T-cell memory. Nat. Rev. Immunol. 2005;5:101–111. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

