Why nature really chose phosphate
- PMID: 23318152
- PMCID: PMC7032660
- DOI: 10.1017/S0033583512000157
Why nature really chose phosphate
Abstract
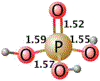
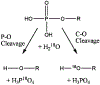
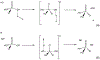
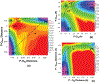
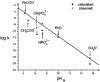
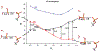
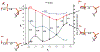
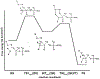
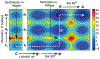
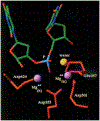
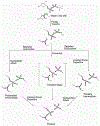
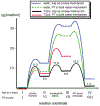
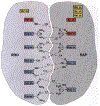
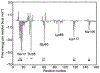
Phosphoryl transfer plays key roles in signaling, energy transduction, protein synthesis, and maintaining the integrity of the genetic material. On the surface, it would appear to be a simple nucleophile displacement reaction. However, this simplicity is deceptive, as, even in aqueous solution, the low-lying d-orbitals on the phosphorus atom allow for eight distinct mechanistic possibilities, before even introducing the complexities of the enzyme catalyzed reactions. To further complicate matters, while powerful, traditional experimental techniques such as the use of linear free-energy relationships (LFER) or measuring isotope effects cannot make unique distinctions between different potential mechanisms. A quarter of a century has passed since Westheimer wrote his seminal review, 'Why Nature Chose Phosphate' (Science 235 (1987), 1173), and a lot has changed in the field since then. The present review revisits this biologically crucial issue, exploring both relevant enzymatic systems as well as the corresponding chemistry in aqueous solution, and demonstrating that the only way key questions in this field are likely to be resolved is through careful theoretical studies (which of course should be able to reproduce all relevant experimental data). Finally, we demonstrate that the reason that nature really chose phosphate is due to interplay between two counteracting effects: on the one hand, phosphates are negatively charged and the resulting charge-charge repulsion with the attacking nucleophile contributes to the very high barrier for hydrolysis, making phosphate esters among the most inert compounds known. However, biology is not only about reducing the barrier to unfavorable chemical reactions. That is, the same charge-charge repulsion that makes phosphate ester hydrolysis so unfavorable also makes it possible to regulate, by exploiting the electrostatics. This means that phosphate ester hydrolysis can not only be turned on, but also be turned off, by fine tuning the electrostatic environment and the present review demonstrates numerous examples where this is the case. Without this capacity for regulation, it would be impossible to have for instance a signaling or metabolic cascade, where the action of each participant is determined by the fine-tuned activity of the previous piece in the production line. This makes phosphate esters the ideal compounds to facilitate life as we know it.
Figures
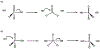
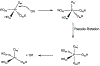
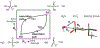

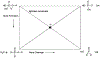

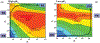
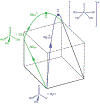
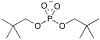
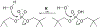



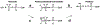
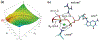






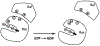

References
-
- Abrahams JP, Leslie AGW, Lutter R & Walker JE (1994). Structure at 2·8 Å resolution of F1-ATPase from bovine heart mitochondria. Nature 370, 621–628. - PubMed
-
- Adachi K, Oiwa K, Nishizaka T, Furuike S, Noji H, Itoh H, Yoshida M & Kinosita K (2007). Coupling of rotation and catalysis in F1-ATPase revealed by single-molecule imaging and manipulation. Cell 130, 309–321. - PubMed
-
- Adams JA (2001). Kinetic and catalytic mechanisms of protein kinases. Chemical Reviews 101, 2271–2290. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

