Surprise maximization reveals the community structure of complex networks
- PMID: 23320141
- PMCID: PMC3544010
- DOI: 10.1038/srep01060
Surprise maximization reveals the community structure of complex networks
Abstract
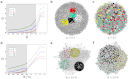
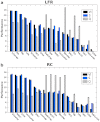
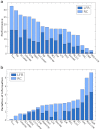
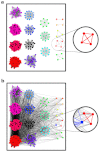
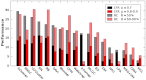
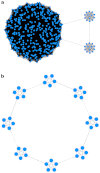
How to determine the community structure of complex networks is an open question. It is critical to establish the best strategies for community detection in networks of unknown structure. Here, using standard synthetic benchmarks, we show that none of the algorithms hitherto developed for community structure characterization perform optimally. Significantly, evaluating the results according to their modularity, the most popular measure of the quality of a partition, systematically provides mistaken solutions. However, a novel quality function, called Surprise, can be used to elucidate which is the optimal division into communities. Consequently, we show that the best strategy to find the community structure of all the networks examined involves choosing among the solutions provided by multiple algorithms the one with the highest Surprise value. We conclude that Surprise maximization precisely reveals the community structure of complex networks.
Figures
References
-
- Wasserman S. & Faust K. Social Network Analysis: Methods and Applications. (Cambridge University Press, 1994).
-
- Strogatz S. H. Exploring complex networks. Nature 410, 268–276 (2001). - PubMed
-
- Barabási A.-L. & Oltvai Z. N. Network biology: understanding the cell's functional organization. Nat. Rev. Genet. 5, 101–113 (2004). - PubMed
-
- Costa L. D. F., Rodrigues F. A., Travieso G. & Boas P. R. V. Characterization of complex networks: A survey of measurements. Adv. Phys. 56, 167 (2007).
-
- Newman M. E. J. Networks: An Introduction (Oxford University Press, 2010).
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

