A computational model for optimal muscle activity considering muscle viscoelasticity in wrist movements

Abstract

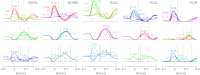
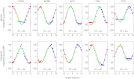
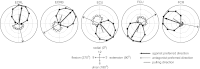
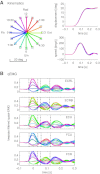
To understand the mechanism of neural motor control, it is important to clarify how the central nervous system organizes the coordination of redundant muscles. Previous studies suggested that muscle activity for step-tracking wrist movements are optimized so as to reduce total effort or end-point variance under neural noise. However, since the muscle dynamics were assumed as a simple linear system, some characteristic patterns of experimental EMG were not seen in the simulated muscle activity of the previous studies. The biological muscle is known to have dynamic properties in which its elasticity and viscosity depend on activation level. The motor control system is supposed to consider the viscoelasticity of the muscles when generating motor command signals. In this study, we present a computational motor control model that can control a musculoskeletal system with nonlinear dynamics. We applied the model to step-tracking wrist movements actuated by five muscles with dynamic viscoelastic properties. To solve the motor redundancy, we designed the control model to generate motor commands that maximize end-point accuracy under signal-dependent noise, while minimizing the squared sum of them. Here, we demonstrate that the muscle activity simulated by our model exhibits spatiotemporal features of experimentally observed muscle activity of human and nonhuman primates. In addition, we show that the movement trajectories resulting from the simulated muscle activity resemble experimentally observed trajectories. These results suggest that, by utilizing inherent viscoelastic properties of the muscles, the neural system may optimize muscle activity to improve motor performance.

Fig. 1.

Schematic block diagram of the motor control model for step-tracking wrist movement. At the beginning of each movement, a target position θ^d is given to the model. Here, the position of the wrist is defined by the vector θ = [θ₁, θ₂]^T, where θ₁ and θ₂ are joint angles of flexion-extension and radial-ulnar deviation, respectively. At every time step t, the model generates a motor command u(t) given a wrist state x(t). The model has 3 main components, the inverse statics model (ISM), feedback controller (FBC), and forward dynamics model (FDM). The ISM generates a time-invariant feedforward motor command u^ism that shifts the wrist's equilibrium to the target position θ^d. At every time step t, the FBC generates a feedback motor command u^fbc(t) that reduces a position error θ^e(t) [= θ^d − θ^p(t)] and its time derivative θ̇^e (t). Here, the vector θ^p(t) is a predicted position that the wrist will reach after T_f seconds from time step t. The predicted position θ^p(t) and its time derivative θ̇^p(t) are predicted by the FDM, given an efference copy of the motor command u(t) and the wrist state x(t). Finally, the sum of u^ism and u^fbc(t) becomes the motor command u(t) sent to the wrist muscles. Note that the state vector of the wrist is defined as x(t) = [θ(t)^T, θ̇(t)^T, a(t)^T, ȧ(t)^T ]^T, where θ̇(t), a(t), and ȧ(t) are a time derivative of the wrist position, muscle activation level, and its time derivative, respectively.

Fig. 2.

Kinematics of step-tracking wrist movements. A: paths of wrist motion. Step-tracking movements started from the neutral position (a black circle) toward 16 radially located targets (black squares). Targets are identified by their clock time positions. Flx, flexion; Ext, extension; Rad, radial deviation; Uln, ulnar deviation. B: time series of wrist displacement from initial position. C: time series of wrist speed (1st time derivative of wrist displacement). D: time series of wrist speed during movements toward four cardinal targets, 3, 6, 9, and 12, extracted from C. Line colors represent the target direction shown in A; 0 s corresponds to the timing of movement onset.

Fig. 3.

Simulated muscle activities. Time series of quantitative (q)EMG signals, motor command signals sent to the 5 muscles, are smoothed by a fourth-order 20-Hz low-pass Butterworth filter and plotted with respect to each of the 5 muscles [from the top, extensor carpi radialis longus (ECRL), extensor carpi radialis brevis (ECRB), extensor carpi ulnaris (ECU), flexor carpi radialis (FCR), and flexor carpi ulnaris (FCU)]. qEMG signals of all 16 step-tracking movements are aligned at movement onset (time = 0 s). Colors of the temporal waveforms represent the target directions shown in Fig. 2A. The time intervals between pairs of vertical dashed lines and vertical dash-dotted lines are, respectively, agonist and antagonist burst intervals of each muscle.

Fig. 4.

Characteristic qEMG patterns. Top row: graphs show amplitude-graded patterns of the agonist bursts of the 5 muscles. Middle row: graphs show the amplitude patterns of the antagonist bursts. Bottom row: graphs show the muscle activation patterns other than the amplitude-graded pattern. Note that temporally shifted patterns can be seen in the activities of FCR in the target directions 6:00, 6:45, and 7:30. The double-burst pattern can be seen in ECU during the movement towards target 7:30. In addition, the shortened early suppression of antagonist burst can be seen in ECRB for target 9:45.

Fig. 5.

Cosine-like tuning of the integrated qEMG. Integrated qEMG during agonist burst intervals (bottom) and antagonist burst intervals (top) are plotted, with colored circles, against target direction. Colors of the circles correspond to the target directions shown in Fig. 2. Note that maximum values of each of the agonist and antagonist integrated qEMG are scaled to 100 for each muscle. Cosine fitting curves on the integrated qEMG are superimposed with black solid lines. Goodness of the cosine fitting, measured by R², is also superimposed.

Fig. 6.

Directional tuning of agonist integrated qEMG in 5 wrist muscles. Integrals of qEMG during agonist bursts interval are plotted as small black circles in polar coordinates. Sign of the integrals is indicated by the type of the circles (filled = positive; unfilled = negative). Bold arrows point toward the agonist preferred directions. Thin arrows indicate the antagonist preferred directions. Gray short bars represent the muscles' pulling directions. Outer circles correspond to the maximum agonist integrated qEMG for 16 step-tracking movements.

Fig. 7.

Simulated movements with isotropic pulling directions. A: movement kinematics. Paths of wrist position, time series of wrist displacement, and time series of wrist speed. B: simulated muscle activities.

Fig. 8.

Features of movements with isotropic and anisotropic muscle pulling directions. A: path curvature against target direction. Path curvature is defined as the maximum deviation from a straight line. B: peak speed against target direction. C: number of muscle activities with temporally shifted, double-burst, shortened early suppression, and their total. D: gap between agonist preferred direction (agoPD) and muscle pulling direction (musclePD) and deviation of antagonist preferred direction (antPD) from direct opposite of agonist preferred direction (agoPD). Both values are the averages among the 5 muscles.

Fig. 9.

Effect of the ISM and FBC on initial movement direction. A: muscle originated stiffness ellipses (solid lines) and initial torque vectors with respect to the ISM command signal (arrows). The size of the stiffness ellipses and torque vectors are rescaled with the same value for all targets. Straight dashed lines connect the neutral position to each of the 8 targets. For clarity, data for only 8 targets are displayed. B: position feedback gain ellipse.