Robust correlation analyses: false positive and power validation using a new open source matlab toolbox
- PMID: 23335907
- PMCID: PMC3541537
- DOI: 10.3389/fpsyg.2012.00606
Robust correlation analyses: false positive and power validation using a new open source matlab toolbox
Abstract
Pearson's correlation measures the strength of the association between two variables. The technique is, however, restricted to linear associations and is overly sensitive to outliers. Indeed, a single outlier can result in a highly inaccurate summary of the data. Yet, it remains the most commonly used measure of association in psychology research. Here we describe a free Matlab((R)) based toolbox (http://sourceforge.net/projects/robustcorrtool/) that computes robust measures of association between two or more random variables: the percentage-bend correlation and skipped-correlations. After illustrating how to use the toolbox, we show that robust methods, where outliers are down weighted or removed and accounted for in significance testing, provide better estimates of the true association with accurate false positive control and without loss of power. The different correlation methods were tested with normal data and normal data contaminated with marginal or bivariate outliers. We report estimates of effect size, false positive rate and power, and advise on which technique to use depending on the data at hand.
Keywords: MATLAB; correlation; outliers; power; robust statistics.
Figures
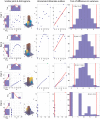
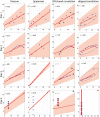
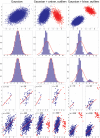
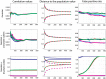


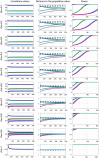
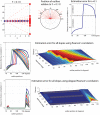
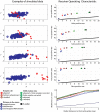
References
-
- Barnett V., Lewis T. (1994). Ouliers in Statistical Data. Chichester: Wiley
-
- Anscombe F. J. (1973). Graphs in statistical analysis. Am. Stat. 27, 17–2110.1080/00031305.1973.10478966 - DOI
-
- Carling K. (2000). Resistant outlier rules and the non-Gaussian case. Stat. Data Anal. 33, 249–25810.1016/S0167-9473(99)00057-2 - DOI
LinkOut - more resources
Full Text Sources
Other Literature Sources

