A virtual retina for studying population coding
- PMID: 23341940
- PMCID: PMC3544815
- DOI: 10.1371/journal.pone.0053363
A virtual retina for studying population coding
Abstract
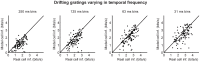
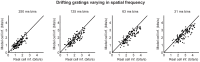
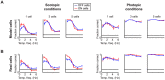
At every level of the visual system - from retina to cortex - information is encoded in the activity of large populations of cells. The populations are not uniform, but contain many different types of cells, each with its own sensitivities to visual stimuli. Understanding the roles of the cell types and how they work together to form collective representations has been a long-standing goal. This goal, though, has been difficult to advance, and, to a large extent, the reason is data limitation. Large numbers of stimulus/response relationships need to be explored, and obtaining enough data to examine even a fraction of them requires a great deal of experiments and animals. Here we describe a tool for addressing this, specifically, at the level of the retina. The tool is a data-driven model of retinal input/output relationships that is effective on a broad range of stimuli - essentially, a virtual retina. The results show that it is highly reliable: (1) the model cells carry the same amount of information as their real cell counterparts, (2) the quality of the information is the same - that is, the posterior stimulus distributions produced by the model cells closely match those of their real cell counterparts, and (3) the model cells are able to make very reliable predictions about the functions of the different retinal output cell types, as measured using Bayesian decoding (electrophysiology) and optomotor performance (behavior). In sum, we present a new tool for studying population coding and test it experimentally. It provides a way to rapidly probe the actions of different cell classes and develop testable predictions. The overall aim is to build constrained theories about population coding and keep the number of experiments and animals to a minimum.
Conflict of interest statement
Figures
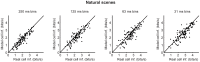




Similar articles
-
Three Small-Receptive-Field Ganglion Cells in the Mouse Retina Are Distinctly Tuned to Size, Speed, and Object Motion.J Neurosci. 2017 Jan 18;37(3):610-625. doi: 10.1523/JNEUROSCI.2804-16.2016. J Neurosci. 2017. PMID: 28100743 Free PMC article.
-
Retinal ganglion cells act largely as independent encoders.Nature. 2001 Jun 7;411(6838):698-701. doi: 10.1038/35079612. Nature. 2001. PMID: 11395773
-
Theoretical understanding of the early visual processes by data compression and data selection.Network. 2006 Dec;17(4):301-34. doi: 10.1080/09548980600931995. Network. 2006. PMID: 17283516 Review.
-
Functional Diversity in the Retina Improves the Population Code.Neural Comput. 2019 Feb;31(2):270-311. doi: 10.1162/neco_a_01158. Epub 2018 Dec 21. Neural Comput. 2019. PMID: 30576618
-
Stimulus-dependent engagement of neural mechanisms for reliable motion detection in the mouse retina.J Neurophysiol. 2018 Sep 1;120(3):1153-1161. doi: 10.1152/jn.00716.2017. Epub 2018 Jun 13. J Neurophysiol. 2018. PMID: 29897862 Free PMC article. Review.
Cited by
-
Receptive Field Vectors of Genetically-Identified Retinal Ganglion Cells Reveal Cell-Type-Dependent Visual Functions.PLoS One. 2016 Feb 4;11(2):e0147738. doi: 10.1371/journal.pone.0147738. eCollection 2016. PLoS One. 2016. PMID: 26845435 Free PMC article.
-
Nonlinear Spatial Integration Underlies the Diversity of Retinal Ganglion Cell Responses to Natural Images.J Neurosci. 2021 Apr 14;41(15):3479-3498. doi: 10.1523/JNEUROSCI.3075-20.2021. Epub 2021 Mar 4. J Neurosci. 2021. PMID: 33664129 Free PMC article.
-
Interacting linear and nonlinear characteristics produce population coding asymmetries between ON and OFF cells in the retina.J Neurosci. 2013 Sep 11;33(37):14958-73. doi: 10.1523/JNEUROSCI.1004-13.2013. J Neurosci. 2013. PMID: 24027295 Free PMC article.
-
Zipf's Law Arises Naturally When There Are Underlying, Unobserved Variables.PLoS Comput Biol. 2016 Dec 20;12(12):e1005110. doi: 10.1371/journal.pcbi.1005110. eCollection 2016 Dec. PLoS Comput Biol. 2016. PMID: 27997544 Free PMC article.
-
Metaheuristic Optimisation Algorithms for Tuning a Bioinspired Retinal Model.Sensors (Basel). 2019 Nov 6;19(22):4834. doi: 10.3390/s19224834. Sensors (Basel). 2019. PMID: 31698827 Free PMC article.
References
-
- Smith DV, John SJ, Boughter JD (2000) Neuronal cell types and taste quality coding. Physiol Behav 69: 77–85. - PubMed
-
- Di Lorenzo PM (2000) The neural code for taste in the brain stem: response profiles. Physiol Behav 69: 87–96. - PubMed
-
- Laurent G (2002) Olfactory network dynamics and the coding of multidimensional signals. Nat Rev Neurosci 3: 884–895. - PubMed
-
- Konishi M (2003) Coding of auditory space. Annu Rev Neurosci 26: 31–55. - PubMed
-
- Field GD, Chichilnisky EJ (2007) Information processing in the primate retina: circuitry and coding. Annu Rev Neurosci 30: 1–30. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

