A Weber-like law for perceptual learning

Abstract

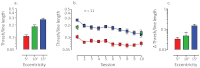
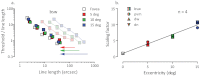
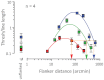
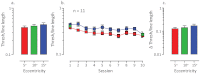
What determines how much an organism can learn? One possibility is that the neural factors that limit sensory performance prior to learning, place an upper limit on the amount of learning that can take place. We tested this idea by comparing learning on a sensory task where performance is limited by cortical mechanisms, at two retinal eccentricities. Prior to learning, visual performance at the two eccentricities was either unmatched or equated in two different ways (through spatial scaling or visual crowding). The magnitude of learning was equivalent when initial levels of performance were matched regardless of how performance was equated. The magnitude of learning was a constant proportion of initial performance. This Weber-like law for perceptual learning demonstrates that it should be possible to predict the degree of perceptual improvement and the final level of performance that can be achieved via sensory training, regardless of what cortical constraint limits performance.

Figure 1. Schematic illustration of stimuli.

Stimuli were always white and presented on a black background, but are shown here and represented in subsequent figures in red (5 deg), green (10 deg) and blue (15 deg). Unscaled stimuli (top row) were the same retinal size at each eccentricity; scaled stimuli (middle row) were larger at more eccentric locations; crowded stimuli (bottom row) were the same size at each eccentricity. As crowding increases with retinal eccentricity, different spatial distances were required between target and flanker to equate performance. Subjects were trained with stimuli presented at 5 and 15 degrees. Vernier alignment threshold at 10 degrees was only measured on the first and last training sessions.

Figure 2. Learning with unscaled stimuli.

Performance on session 1 (a) at 5, 10 and 15 degrees. (b) Mean learning curves for 11 subjects at 5 and 15 degrees. Data for 10 degrees, where no training took place, is shown for session 1 and 10. (c) Improvement in performance at each eccentricity. Improvement is quantified as the difference between performance on the first and final sessions. Data for 5, 10 and 15 degrees are shown in red, green and blue, respectively. Initial performance drops with increases in retinal eccentricity. However, improvement in performance generated by training on the task across 10 sessions increases with retinal eccentricity. Error bars represent 1 standard error of the mean (SEM).

Figure 3. Spatially scaling stimuli equates peripheral to foveal Vernier alignment thresholds.

Weber fractions for the fovea and 3 eccentric locations are plotted (data shown in lower contrast) as a function of line length for a representative subject. (a) A scaling factor that minimised the mean squared error between the eccentric and foveal data (see high contrast data points) was calculated. (b) A linear regression line fitted through the data estimates the scaling factor required to increase the size of the eccentric stimuli such that performance is matched to that at the fovea. dw and dn are data reproduced from Whitaker et al., (1992).

Figure 4. Learning with spatially scaled stimuli.

(a) Performance on session 1 at 5, 10 and 15 degrees. (b) Learning curves showing mean performance on each session at 5 and 15 degrees. Data for 10 degrees, where no training took place, is shown for session 1 and 10. (c) Improvement in performance at each eccentricity. Improvement is quantified as the difference between performance on the first and final sessions. Data for 5, 10 and 15 degrees is shown in red, green and blue, respectively. Performance at each eccentricity is the same on session 1 and there is no significant difference in improvement at each eccentricity. Error bars represent 1 standard error of the mean (SEM).

Figure 5. The effect of flanker distance on Vernier alignment at each eccentricity.

Mean vernier threshold/line length at 5 (red), 10 (green) and 15 (blue) degrees plotted for 4 subjects as a function flanker distance. Smooth curves are best fitting solutions of Equation 1. Flanker distances were estimated from each curve that corresponded to the same threshold (yellow lines).

Figure 6. Learning with crowded stimuli.

(a) Performance on session 1 at 5, 10 and 15 degrees. (b) Learning curves showing mean performance on each session at 5 and 15 degrees, with data for 10 degrees shown for the first and final session. (c) Improvement in performance at each eccentricity. Performance at each eccentricity is the same on session 1 and there is no significant difference in the magnitude of improvement across eccentricities. Error bars as before.

Figure 7. Improvement in performance as a function of starting performance.

Improvement at 5 (red), 10 (green) and 15 degrees (blue), expressed as the difference in performance between the first and final session. (a) The curve shows best fitting solutions Equation 2 with a slope 1.007 and intercept −0.42. Improvements are a constant proportion (approximately 0.38) of starting performance. (b) Improvements plotted as a ratio between the final and first session. (c) Measured final session performance plotted as a function of final session performance as predicted by applying a universal improvement factor of 2.18.