Overview of current methods in sedimentation velocity and sedimentation equilibrium analytical ultracentrifugation

Abstract

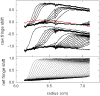
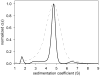
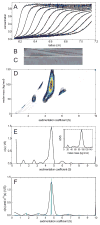
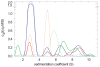
Modern computational strategies have allowed for the direct modeling of the sedimentation process of heterogeneous mixtures, resulting in sedimentation velocity (SV) size-distribution analyses with significantly improved detection limits and strongly enhanced resolution. These advances have transformed the practice of SV, rendering it the primary method of choice for most existing applications of analytical ultracentrifugation (AUC), such as the study of protein self- and hetero-association, the study of membrane proteins, and applications in biotechnology. New global multisignal modeling and mass conservation approaches in SV and sedimentation equilibrium (SE), in conjunction with the effective-particle framework for interpreting the sedimentation boundary structure of interacting systems, as well as tools for explicit modeling of the reaction/diffusion/sedimentation equations to experimental data, have led to more robust and more powerful strategies for the study of reversible protein interactions and multiprotein complexes. Furthermore, modern mathematical modeling capabilities have allowed for a detailed description of many experimental aspects of the acquired data, thus enabling novel experimental opportunities, with important implications for both sample preparation and data acquisition. The goal of the current unit is to describe the current tools for the study of soluble proteins, detergent-solubilized membrane proteins and their interactions by SV and SE.

Figure 1

Examples for the shapes of Lamm equation solutions. The profiles are calculated for particles of different size and sedimentation properties. All conditions are calculated for a rotor speed of 50,000 rpm, and 50 concentration profiles are shown at different (in each case equally spaced) time intervals. Later scans are indicated by a higher color temperature. (A) Small molecules with a sedimentation coefficient of 0.2 S and a diffusion coefficient of 6×10⁻⁶ cm²/sec, in Δt = 300 sec intervals. Similar values are frequently observed for sedimenting buffer salts. (B) Sedimentation of a peptide of 1 kg/mol and 0.3 S, Δt = 1000 sec. (C) A small protein of 10 kg/mol and 1.5 S, Δt = 500 sec. (D) A protein of 100 kg/mol and 6 S, Δt = 300 sec. (E) Particle of 1 Mg/mol and 30 S, Δt = 50 sec. (F) A floating particle with a sedimentation coefficient of −3.0 S and a diffusion coefficient of 2.71×10⁻⁷ cm²/sec. Such data patterns may be obtained, for example, with large emulsion or lipid particles. In flotation, the radial dilution is replaced with radial increase in concentration in the plateau region of successive profiles. (Figure reproduced from (Schuck, 2012).)

Figure 2

Demonstration of interference optical data before (top) and after (bottom) subtracting the estimated TI and RI noise contributions. Both the time-dependent (radius-invariant, RI) signal offsets arising from jitter and integral fringe shifts, as well as the radius-dependent (time-invariant, TI) signal offset arising from imperfections in the smoothness of the optical elements, can be clearly discerned. After fitting the data with a model including terms for TI and RI noise, the best-fit values for the TI noise (red line in top panel) and for the RI noise (not shown) can be subtracted from the raw data, as shown in the lower panel. As long as the degrees of freedom for unknown TI and RI noise are maintained in the further analysis, this subtraction does not alter the information content of the data, but allows better visual inspection of the signal from the macromolecular redistribution. (Figure reproduced from Curr. Protoc. Immunol., Chapter 18, Unit 18 15 (2008)).

Figure 3

c(s) distribution of the data shown in Figure 2. For comparison, the dashed line shows the ls-g*(s) distribution derived from a subset of the scans.

Figure 4

Example of SV analyses of a system with non-interacting species. (A) Representative subset of the raw data after elimination of systematic noise contributions. (B) Residuals bitmap from a fit with insufficient quality: the data in (A) are modeled with an impostor single-species fit, resulting in clearly systematic deviations that can be discerned from the strong diagonal feature in the bitmap. (C) The quality of the fit with a c(s) model results in a residuals bitmap with very few diagonal features. There are some vertical and horizontal lines indicative of the remaining residuals due to technical imperfections in the data acquisition process, such as higher-order vibrations of optical components. (D) Size and-shape distribution, transformed into coordinates of sedimentation coefficient and molar mass. The color temperature of the contour lines indicates the population of species. Like in one-dimensional c(s), the peak-width in c(s,M) contains contributions both from regularization (reflecting limited resolution given the signal-to-noise ratio of the data) and from true heterogeneity. (E) Reduction of the c(s,M) distribution to a pure sedimentation coefficient distribution, general c(s,*). This is equivalent to a conventional c(s) analysis but without any constraints to a common average frictional ratio of all species. The inset shows a pure molar-mass distribution, c(M,*), also derived by integration of c(s,M) in a direction orthogonal to c(s,*). (F) Size distribution c(s) using a hydrodynamic scaling law (black line with broad peaks). Also shown is the result of a Bayesian analysis using prior knowledge in the analysis of this non-interacting system, here in the form of c^(Pδ)(s) (blue line with sharp peaks) using the hypothesis that the sample consists of discrete species. Generally, the peak width in c(s) can result from either a true polydispersity of the protein (e.g., strong heterogeneity in glycosylation, in conformation, primary sequence, etc.), or from the standard regularization favoring broader peaks for data with low signal/noise ratio. (Figure reproduced from (Schuck et al., 2010).)

Figure 5

Example of the multi-signal c_k(s) analysis of a triple protein mixture of a viral glycoprotein (green), its cognate receptor (blue), and a heterogeneous antigen-recognition receptor fragment (red). The content of each protein component in the different s-ranges is obtained from the global analysis of sedimentation data acquired with the interference optics and with the absorbance system at two different wavelengths (data not shown), using two chromophorically labeled proteins and one unlabeled protein. Solid lines show the c_k(s) analysis of the triple mixture. The analogous distributions of each protein alone are shown as dashed lines. The formation of two coexisting binary complexes at ~5 S and ~7 S and a ternary complex with 1:1:1 stoichiometry at ~8.5 S can be discerned. Figure reproduced from (Schuck et al., 2010).

Figure 6

Properties of the reaction boundary A···B as a function of the total loading concentration of A and B, calculated by EPT for the system of Figure 1. (Top) Velocity of the reaction boundary s_A···B following Eq. 6. (Middle) Composition R_A···B of the reaction boundary following Eq. 7. (Bottom) Fractional signal of the undisturbed boundary, assuming that both components are globular with equal weight-based extinction coefficients. In all plots the line for the phase transition c_Btot^*(c_Atot) is shown as black dotted line, separating the region of A···(B) in the upper left quadrant from B (A) elsewhere. Figure reproduced from (Schuck, 2010b).