Flexible parametric modelling of cause-specific hazards to estimate cumulative incidence functions

Abstract

Background: Competing risks are a common occurrence in survival analysis. They arise when a patient is at risk of more than one mutually exclusive event, such as death from different causes, and the occurrence of one of these may prevent any other event from ever happening.

Methods: There are two main approaches to modelling competing risks: the first is to model the cause-specific hazards and transform these to the cumulative incidence function; the second is to model directly on a transformation of the cumulative incidence function. We focus on the first approach in this paper. This paper advocates the use of the flexible parametric survival model in this competing risk framework.

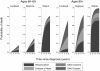
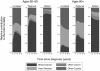
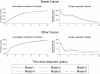
Results: An illustrative example on the survival of breast cancer patients has shown that the flexible parametric proportional hazards model has almost perfect agreement with the Cox proportional hazards model. However, the large epidemiological data set used here shows clear evidence of non-proportional hazards. The flexible parametric model is able to adequately account for these through the incorporation of time-dependent effects.

Conclusion: A key advantage of using this approach is that smooth estimates of both the cause-specific hazard rates and the cumulative incidence functions can be obtained. It is also relatively easy to incorporate time-dependent effects which are commonly seen in epidemiological studies.

Figure 1

Comparison of Cox proportional hazards model (Cox) and flexible parametric proportional hazards model (FPM) for ages 60–69. Note: breast cancer is on a different scale.

Figure 2

Cause-specific hazard functions by breast cancer stage for ages 60–69 taken from the flexible parametric proportional hazards model.

Figure 3

Comparison of proportional hazards model (PH) and model incorporating time-dependent effects (TD) using the flexible parametric survival model for ages 60–69. Note that the plots for breast cancer and other cancer are on different scales.

Figure 4

Stacked cumulative incidence function plots by stage for ages 60–69 and 80 + .

Figure 5

Relative contribution to the total mortality by stage for ages 60–69 and 80 + .

Figure 6

Relative contribution to the overall hazard by stage for ages 60–69 and 80 + .

Figure 7

Comparison of 95 per cent confidence intervals for the cumulative incidence function using the delta method (dashed lines) and bootstrapping (shaded area). Note: breast cancer is on a different scale.

Figure 8

Comparison of models with varying numbers of knots for distant stage, ages 60–69. Note that, although there are 6 curves plotted on the graph, 5 curves are overlaying on the cause-specific hazard plots and only model 6 differs from the other models.