Interpreting motion and force for narrow-band intermodulation atomic force microscopy
- PMID: 23400552
- PMCID: PMC3566785
- DOI: 10.3762/bjnano.4.5
Interpreting motion and force for narrow-band intermodulation atomic force microscopy
Abstract
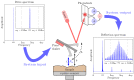
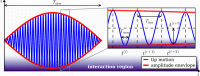
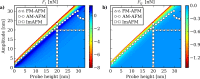
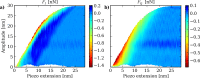
Intermodulation atomic force microscopy (ImAFM) is a mode of dynamic atomic force microscopy that probes the nonlinear tip-surface force by measurement of the mixing of multiple modes in a frequency comb. A high-quality factor cantilever resonance and a suitable drive comb will result in tip motion described by a narrow-band frequency comb. We show, by a separation of time scales, that such motion is equivalent to rapid oscillations at the cantilever resonance with a slow amplitude and phase or frequency modulation. With this time-domain perspective, we analyze single oscillation cycles in ImAFM to extract the Fourier components of the tip-surface force that are in-phase with the tip motion (F(I)) and quadrature to the motion (F(Q)). Traditionally, these force components have been considered as a function of the static-probe height only. Here we show that F(I) and F(Q) actually depend on both static-probe height and oscillation amplitude. We demonstrate on simulated data how to reconstruct the amplitude dependence of F(I) and F(Q) from a single ImAFM measurement. Furthermore, we introduce ImAFM approach measurements with which we reconstruct the full amplitude and probe-height dependence of the force components F(I) and F(Q), providing deeper insight into the tip-surface interaction. We demonstrate the capabilities of ImAFM approach measurements on a polystyrene polymer surface.
Keywords: AFM; atomic force microscopy; force spectroscopy; frequency combs; high-quality-factor resonators; intermodulation; multifrequency.
Figures
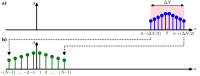
 =
=  Δω, in a bandwidth that is given by the integer number ΔN. The spectrum of the corresponding time-dependent envelope function (b) is obtained by down-shifting the original spectrum in frequency space such that the shifted center frequency is zero.
Δω, in a bandwidth that is given by the integer number ΔN. The spectrum of the corresponding time-dependent envelope function (b) is obtained by down-shifting the original spectrum in frequency space such that the shifted center frequency is zero.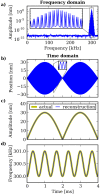

References
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous
