Structural constraints on the three-dimensional geometry of simple viruses: case studies of a new predictive tool
- PMID: 23403965
- PMCID: PMC3571114
- DOI: 10.1107/S0108767312047150
Structural constraints on the three-dimensional geometry of simple viruses: case studies of a new predictive tool
Abstract
Understanding the fundamental principles of virus architecture is one of the most important challenges in biology and medicine. Crick and Watson were the first to propose that viruses exhibit symmetry in the organization of their protein containers for reasons of genetic economy. Based on this, Caspar and Klug introduced quasi-equivalence theory to predict the relative locations of the coat proteins within these containers and classified virus structure in terms of T-numbers. Here it is shown that quasi-equivalence is part of a wider set of structural constraints on virus structure. These constraints can be formulated using an extension of the underlying symmetry group and this is demonstrated with a number of case studies. This new concept in virus biology provides for the first time predictive information on the structural constraints on coat protein and genome topography, and reveals a previously unrecognized structural interdependence of the shapes and sizes of different viral components. It opens up the possibility of distinguishing the structures of different viruses with the same T-number, suggesting a refined viral structure classification scheme. It can moreover be used as a basis for models of virus function, e.g. to characterize the start and end configurations of a structural transition important for infection.
Keywords: affine-extended symmetry group; genome organization; structural constraints; tiling theory; virus structure.
Figures
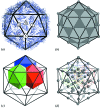
 surface lattice from quasi-equivalence theory that encodes the protein organizations in capsids composed of
surface lattice from quasi-equivalence theory that encodes the protein organizations in capsids composed of  coat proteins. (c), (d) A packing of overlapping icosahedra generates a partition of the icosahedral face akin to the
coat proteins. (c), (d) A packing of overlapping icosahedra generates a partition of the icosahedral face akin to the  structure: (c) shows three of the
structure: (c) shows three of the  translated and rotated icosahedra as solids; (d) shows the edges of these icosahedra, together with the vertices of all 60 icosahedra. This is an example of the structural constraints implied by our theory.
translated and rotated icosahedra as solids; (d) shows the edges of these icosahedra, together with the vertices of all 60 icosahedra. This is an example of the structural constraints implied by our theory.



Similar articles
-
Affine extensions of the icosahedral group with applications to the three-dimensional organisation of simple viruses.J Math Biol. 2009 Sep;59(3):287-313. doi: 10.1007/s00285-008-0228-5. Epub 2008 Nov 1. J Math Biol. 2009. PMID: 18979101
-
Measurements of the self-assembly kinetics of individual viral capsids around their RNA genome.Proc Natl Acad Sci U S A. 2019 Nov 5;116(45):22485-22490. doi: 10.1073/pnas.1909223116. Epub 2019 Sep 30. Proc Natl Acad Sci U S A. 2019. PMID: 31570619 Free PMC article.
-
The structure of bacteriophage phiCb5 reveals a role of the RNA genome and metal ions in particle stability and assembly.J Mol Biol. 2009 Aug 21;391(3):635-47. doi: 10.1016/j.jmb.2009.06.047. Epub 2009 Jun 23. J Mol Biol. 2009. PMID: 19559027
-
What does structure tell us about virus evolution?Curr Opin Struct Biol. 2005 Dec;15(6):655-63. doi: 10.1016/j.sbi.2005.10.012. Epub 2005 Nov 3. Curr Opin Struct Biol. 2005. PMID: 16271469 Review.
-
Principles of virus structural organization.Adv Exp Med Biol. 2012;726:17-47. doi: 10.1007/978-1-4614-0980-9_3. Adv Exp Med Biol. 2012. PMID: 22297509 Free PMC article. Review.
Cited by
-
Origami and materials science.Philos Trans A Math Phys Eng Sci. 2021 Jul 12;379(2201):20200113. doi: 10.1098/rsta.2020.0113. Epub 2021 May 24. Philos Trans A Math Phys Eng Sci. 2021. PMID: 34024126 Free PMC article.
-
A multiscale model of virus pandemic: Heterogeneous interactive entities in a globally connected world.Math Models Methods Appl Sci. 2020 Jul;30(8):1591-1651. doi: 10.1142/s0218202520500323. Epub 2020 Aug 19. Math Models Methods Appl Sci. 2020. PMID: 35309741 Free PMC article.
-
Explicit description of viral capsid subunit shapes by unfolding dihedrons.Commun Biol. 2024 Nov 14;7(1):1509. doi: 10.1038/s42003-024-07218-x. Commun Biol. 2024. PMID: 39543373 Free PMC article.
-
Protruding Features of Viral Capsids Are Clustered on Icosahedral Great Circles.PLoS One. 2016 Apr 5;11(4):e0152319. doi: 10.1371/journal.pone.0152319. eCollection 2016. PLoS One. 2016. PMID: 27045511 Free PMC article.
-
Dynamic Assembly of Pentamer-Based Protein Nanotubes.ACS Nano. 2025 Mar 11;19(9):8786-8798. doi: 10.1021/acsnano.4c16192. Epub 2025 Feb 24. ACS Nano. 2025. PMID: 39993171 Free PMC article.
References
-
- Bamford, D. H., Grimes, J. M. & Stuart, D. I. (2005). Curr. Opin. Struct. Biol. 15, 655–663. - PubMed
-
- Bruijn, N. G. de (1981a). Nederl. Akad. Wetensch. Indag. Math. 43, 39–52.
-
- Bruijn, N. G. de (1981b). Nederl. Akad. Wetensch. Indag. Math. 43, 53–66.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
