A model-based approach to trial-by-trial p300 amplitude fluctuations
- PMID: 23404628
- PMCID: PMC3567611
- DOI: 10.3389/fnhum.2012.00359
A model-based approach to trial-by-trial p300 amplitude fluctuations
Abstract
It has long been recognized that the amplitude of the P300 component of event-related brain potentials is sensitive to the degree to which eliciting stimuli are surprising to the observers (Donchin, 1981). While Squires et al. (1976) showed and modeled dependencies of P300 amplitudes from observed stimuli on various time scales, Mars et al. (2008) proposed a computational model keeping track of stimulus probabilities on a long-term time scale. We suggest here a computational model which integrates prior information with short-term, long-term, and alternation-based experiential influences on P300 amplitude fluctuations. To evaluate the new model, we measured trial-by-trial P300 amplitude fluctuations in a simple two-choice response time task, and tested the computational models of trial-by-trial P300 amplitudes using Bayesian model evaluation. The results reveal that the new digital filtering (DIF) model provides a superior account of the trial-by-trial P300 amplitudes when compared to both Squires et al.'s (1976) model, and Mars et al.'s (2008) model. We show that the P300-generating system can be described as two parallel first-order infinite impulse response (IIR) low-pass filters and an additional fourth-order finite impulse response (FIR) high-pass filter. Implications of the acquired data are discussed with regard to the neurobiological distinction between short-term, long-term, and working memory as well as from the point of view of predictive coding models and Bayesian learning theories of cortical function.
Keywords: Bayesian surprise; P300; digital filtering; event-related brain potentials; predictive surprise; single trial EEG.
Figures


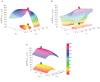
 denote a delay of one trial. At the adder element ⊕, updating of the weighted output γS·cS,k(n − 1) of the last trial n − 1 with the weighted input (1 − γS)·gk(n − 1) of the last trial results in the current output cS,k(n). Note that via γS·cS,k(n − 1), all preceding inputs (and outputs) influence the current output, though for the short-term memory, the influence of trials not in the recent past is negligible.
denote a delay of one trial. At the adder element ⊕, updating of the weighted output γS·cS,k(n − 1) of the last trial n − 1 with the weighted input (1 − γS)·gk(n − 1) of the last trial results in the current output cS,k(n). Note that via γS·cS,k(n − 1), all preceding inputs (and outputs) influence the current output, though for the short-term memory, the influence of trials not in the recent past is negligible.
 denote a delay of one trial. At the adder element ⊕, updating of the weighted output γL,n−1·cL,k(n − 1) of the last trial n − 1 with the weighted input (1 − γL,n−1)·gk(n − 1) of the last trial results in the current output cL,k(n). Note that via γL,n−1·cL,k(n − 1), all preceding inputs (and outputs) influence the current output.
denote a delay of one trial. At the adder element ⊕, updating of the weighted output γL,n−1·cL,k(n − 1) of the last trial n − 1 with the weighted input (1 − γL,n−1)·gk(n − 1) of the last trial results in the current output cL,k(n). Note that via γL,n−1·cL,k(n − 1), all preceding inputs (and outputs) influence the current output.

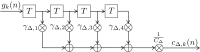
 represent a delay of one trial, the multipliers γΔ,i compose the filter coefficients and CΔ constitutes a normalizing constant.
represent a delay of one trial, the multipliers γΔ,i compose the filter coefficients and CΔ constitutes a normalizing constant.

References
-
- Alba J. W., Chromiak W., Hasher L., Attig M. S. (1980). Automatic encoding of category size information. J. Exp. Psychol. Hum. Learn. 6, 370–37810.1037/0278-7393.6.4.370 - DOI
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

