Self-similarity of contact line depinning from textured surfaces
- PMID: 23422660
- PMCID: PMC3586717
- DOI: 10.1038/ncomms2482
Self-similarity of contact line depinning from textured surfaces
Abstract
The mobility of drops on surfaces is important in many biological and industrial processes, but the phenomena governing their adhesion, which is dictated by the morphology of the three-phase contact line, remain unclear. Here we describe a technique for measuring the dynamic behaviour of the three-phase contact line at micron length scales using environmental scanning electron microscopy. We examine a superhydrophobic surface on which a drop's adhesion is governed by capillary bridges at the receding contact line. We measure the microscale receding contact angle of each bridge and show that the Gibbs criterion is satisfied at the microscale. We reveal a hitherto unknown self-similar depinning mechanism that shows how some hierarchical textures such as lotus leaves lead to reduced pinning, and counter-intuitively, how some lead to increased pinning. We develop a model to predict adhesion force and experimentally verify the model's broad applicability on both synthetic and natural textured surfaces.
Figures



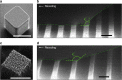
 =145°±3°). Scale bar, 20 μm. See Supplementary Movie 4.
=145°±3°). Scale bar, 20 μm. See Supplementary Movie 4.
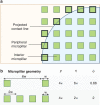

 . Dotted line indicates the normalized force as predicted by equation (4). Error bars indicate s.e.
. Dotted line indicates the normalized force as predicted by equation (4). Error bars indicate s.e.References
-
- Prakash M., Quéré D. & Bush J. W. M.. Surface tension transport of prey by feeding shorebirds: the capillary ratchet. Science 320, 931–934 (2008) . - PubMed
-
- Zheng Y., Gao X. & Jiang L.. Directional adhesion of superhydrophobic butterfly wings. Soft Matter 3, 178–182 (2007) . - PubMed
-
- Zheng Y. et al.. Directional water collection on wetted spider silk. Nature 463, 640–643 (2010) . - PubMed
-
- Dussan V. E. B. & Davis S. H.. On the motion of a fluid-fluid interface along a solid surface. J. Fluid Mech. 65, 71–95 (1974) .
-
- Carey V. P.. Liquid Vapor Phase Change Phenomena: An Introduction to the Thermophysics of Vaporization and Condensation Processes in Heat Transfer Equipment 2nd edn Taylor & Francis (2007) .
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

