Actin cytoskeleton of chemotactic amoebae operates close to the onset of oscillations

Abstract

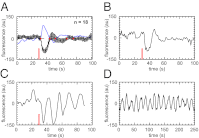
The rapid reorganization of the actin cytoskeleton in response to external stimuli is an essential property of many motile eukaryotic cells. Here, we report evidence that the actin machinery of chemotactic Dictyostelium cells operates close to an oscillatory instability. When averaging the actin response of many cells to a short pulse of the chemoattractant cAMP, we observed a transient accumulation of cortical actin reminiscent of a damped oscillation. At the single-cell level, however, the response dynamics ranged from short, strongly damped responses to slowly decaying, weakly damped oscillations. Furthermore, in a small subpopulation, we observed self-sustained oscillations in the cortical F-actin concentration. To substantiate that an oscillatory mechanism governs the actin dynamics in these cells, we systematically exposed a large number of cells to periodic pulse trains of different frequencies. Our results indicate a resonance peak at a stimulation period of around 20 s. We propose a delayed feedback model that explains our experimental findings based on a time-delay in the regulatory network of the actin system. To test the model, we performed stimulation experiments with cells that express GFP-tagged fusion proteins of Coronin and actin-interacting protein 1, as well as knockout mutants that lack Coronin and actin-interacting protein 1. These actin-binding proteins enhance the disassembly of actin filaments and thus allow us to estimate the delay time in the regulatory feedback loop. Based on this independent estimate, our model predicts an intrinsic period of 20 s, which agrees with the resonance observed in our periodic stimulation experiments.

Fig. 1.

(A) Geometry of the uncaging region (red line) and the imaging region (black square). The small blue square indicates the positions at which the time profile of the fluorescence signal, displayed in B, was evaluated. (B) Time profile of the fluorescence signal (black circles) at a distance of 30 μm downstream of the uncaging line following the release of caged fluorescein by a 1 s laser pulse starting at t = 0 s. The SD in y-direction and time is displayed. Finite element simulations (blue line) provide a good approximation of the fluorescence profile.

Fig. 2.

(A) Average cortical (blue) and cytosolic (black) LimE–GFP fluorescence signal in response to a short pulse (red) of cAMP. The response time scales were defined by the crossings of the cytosolic signal with the averaged lower confidence interval (dashed line, crossings highlighted by red dots). The averaged confidence interval was calculated from the individual confidence intervals of each data point before the pulse was applied (black error bars). (B–D) Time traces of the cytosolic signal from three different single cells. (B) Example of a strongly damped response to a short pulse of cAMP. (C) Example of a weakly damped response to a short pulse of cAMP. (D) Example of a cell that displays self-sustained oscillations in absence of an external stimulus.

Fig. 3.

Time series of the average cytosolic fluorescence intensity (black) of LimE–GFP cells responding to pulse trains with a period of (A) 10 s, (B) 20 s, and (C) 30 s. The laser stimulus is shown in red. The corresponding frequency spectra are displayed in D–F, where the frequency of the external stimulus is marked in red.

Fig. 4.

(A) For each stimulus frequency the amplitude of the largest peak in the frequency spectrum of the corresponding data set is displayed (red triangles). Furthermore, the amplitude at the stimulus frequency is shown (dashed line, not necessarily identical to the frequency of the largest peak). A clear resonance is observed at around stimulation periods of T = 20 s. (B) The first and second harmonics are shown as dashed lines. Black dots indicate the response periods that correspond to the largest and second largest peaks in the response frequency spectra. (C) Time lag between the stimulus and the maximal response of the cytosolic fluorescence intensity. The error bars show the SD across all single-cell experiments available for the respective stimulation period. Note that the time lag is only defined within one stimulation period T and measured between 0 and T, the dashed blue line indicating the maximal lag.

Fig. 5.

Stimulation of labeled cell lines and the corresponding knockouts with a period of 20 s (red). All markers were recorded in independent experiments, and the average cytosolic fluorescence intensities are displayed. (A) Comparison of the responses of LimE–GFP (black) and Coronin–GFP (blue). (B) Comparison of LimE–GFP response in the wild-type (black solid lines) and LimE–GFP response in Coronin-null (black dashed line). (C) Comparison of the response of LimE–GFP (black) and Aip1–GFP (orange). (D) Comparison of LimE–GFP response in the wild-type (black solid lines) and LimE–GFP response in Aip1-null (black dashed-dotted line). (E–H) The corresponding frequency spectra are shown, with n denoting the number of single-cell recordings.

Fig. 6.

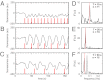
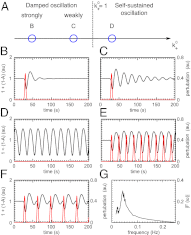
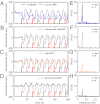
Numerical simulations of model Eq. 1. (A) Phase diagram indicating the different dynamical regimes. The oscillatory instability occurs at and is marked by the dashed vertical line. The different response patterns displayed in Fig. 2 correspond to different values of the bifurcation parameter in the model. (B) Far from the bifurcation point , (C) close to the bifurcation point , and (D) beyond the bifurcation point in the oscillator regime . (E and F) Simulations of periodic stimulation with pulse trains of period T = 20 s (E) and T = 35 s (F), in both cases. (B–F) The red curves show the receptor stimulus, whereas the black curves show the evolution of the cortical actin concentration A(t) over time. For comparison with the experimental data, where the detrended cytosolic signal was displayed, we have plotted 1+(1−A). (G) Resonance curve for periodic stimuli ranging from T = 4–60 s. See Materials and Methods for details on how the receptor stimulus is incorporated into the model.