Identification of the contribution of the ankle and hip joints to multi-segmental balance control

Abstract

Background: Human stance involves multiple segments, including the legs and trunk, and requires coordinated actions of both. A novel method was developed that reliably estimates the contribution of the left and right leg (i.e., the ankle and hip joints) to the balance control of individual subjects.

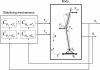
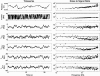
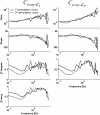
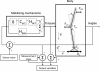
Methods: The method was evaluated using simulations of a double-inverted pendulum model and the applicability was demonstrated with an experiment with seven healthy and one Parkinsonian participant. Model simulations indicated that two perturbations are required to reliably estimate the dynamics of a double-inverted pendulum balance control system. In the experiment, two multisine perturbation signals were applied simultaneously. The balance control system dynamic behaviour of the participants was estimated by Frequency Response Functions (FRFs), which relate ankle and hip joint angles to joint torques, using a multivariate closed-loop system identification technique.

Results: In the model simulations, the FRFs were reliably estimated, also in the presence of realistic levels of noise. In the experiment, the participants responded consistently to the perturbations, indicated by low noise-to-signal ratios of the ankle angle (0.24), hip angle (0.28), ankle torque (0.07), and hip torque (0.33). The developed method could detect that the Parkinson patient controlled his balance asymmetrically, that is, the right ankle and hip joints produced more corrective torque.

Conclusion: The method allows for a reliable estimate of the multisegmental feedback mechanism that stabilizes stance, of individual participants and of separate legs.

Figure 1

Multiple-Input-Multiple-Output closed-loop balance control system. The body mechanics represent the dynamics of a double-inverted pendulum with the corrective ankle and hip torques as inputs and the joint angles as outputs. The stabilizing mechanisms represent the dynamics of the combination of active and passive feedback pathways of the concerned body(part) and generates a torque to correct for the deviation of upright stance. The balance control model can be perturbed with support surface movements (S_x), perturbation forces at the hip (Fp₁) or at the shoulder (Fp₂). Positive torques and positive angles are defined as counterclockwise.

Figure 2

Experimental set-up. The participant stands on the dual forceplate (A) embedded in the movement platform (B). Two independent perturbations are applied with the movement platform (B) and the pusher (C) in the forward-backward direction. Interaction forces between the pusher (C) and the participant are measured with a force sensor (D). Actual falls are prevented by the safety harness (E). Reflective spherical markers (F) measure the movements of the participant.

Figure 3

Theoretical transfer function and estimated frequency response functions $\left(C_{{\mathit{\theta }}_A\to T_A}\mathbf{,}{C}_{{\mathit{\theta }}_A\to T_H}\mathbf{,}{C}_{{\mathit{\theta }}_H\to T_A}\mathbf{\text{and}}{C}_{{\mathit{\theta }}_H\to T_H}\right)$. Results of the model simulations in the presence of pink and white noise during the condition with a platform acceleration and perturbation torque around the ankle are depicted (PLT-N; open dots) and during the condition with one perturbation (PL-N; solid grey dots). The bold solid line represents the model transfer function of the stabilizing mechanisms. Applying two independent perturbations in combination with a multivariate closed-loop system identification method resulted in a correct estimation of the stabilizing mechanisms (FRF 2 perturbations, indicated with open dots), whereas one perturbation resulted in an erroneous estimate (FRF 1 perturbation, indicated with solid grey dots).

Figure 4

Timeseries (left panels) and NSRs (right panels) of the first perturbation round of one representative participant. From top to bottom: platform perturbation, pusher perturbation, ankle angle, hip angle, sway angle, ankle torque, and hip torque. The mean is depicted by the solid line and the standard deviation over the eight cycles by the grey area. The black line in the right panels depicts NSR=1. Ideally, the average NSR of the responses remains below one. The responses of the participant were consistent, as evidenced by small standard deviations over the adjacent segments and low NSRs. This means that a large part of the data is captured by the time-invariant MIMO system identification technique.

Figure 5

Single-Input-Single-Output frequency response functions and coherences of first and second perturbation round. The left panel depicts the FRF from the sway angle to the ankle joint torque; the right panel the FRF from the sway angle to the hip joint torque. The lower panels show the coherence between the perturbation, and the ankle joint torque, hip joint torque, and the sway angle. Similar gains and phases of the frequency response functions of the first and second perturbation round indicate that participants did not change their balance control strategy.

Figure 6

Multiple-Input-Multiple-Output frequency response functions of the stabilizing mechanisms. The solid line represents the average of the healthy participants, with the shaded area indicating the 95% confidence interval and the dotted line the Parkinson patient.

Figure 7

The average contribution of the right leg of the healthy controls and of the PD patient to each Multiple-Input-Multiple-Output frequency response function. The average contribution of the right leg for the healthy controls (HC) is shown by the solid line (mean) and the grey area (95% confidence interval). The patient (dashed line) clearly controlled his balance asymmetrically, with the right leg producing more corrective torque than the left leg to resist the perturbations.

Figure 8

Model of human balance control. The model consists of body mechanics and a controller with intrinsic stiffness and damping (C_pas), an active proportional derivative controller (C_act), timedelays (δ), muscle activation dynamics (H_act), sensor and measurement noise. T_ank and T_hip denote the respective joint torques, θ₁ and θ₂ the joint angles. S_x and F_pert are the force and platform perturbations, respectively. g is the gravitational acceleration.