Collective diffusion model for ion conduction through microscopic channels

Abstract

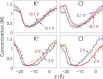
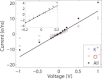
Ion conduction through microscopic channels is of central importance in both biology and nanotechnology. To better understand the current-voltage (I-V) dependence of ion channels, here we describe and prove a collective diffusion model that quantitatively relates the spontaneous ion permeation at equilibrium to the stationary ionic fluxes driven by small voltages. The model makes it possible to determine the channel conductance in the linear I-V range from equilibrium simulations without the application of a voltage. To validate the theory, we perform molecular-dynamics simulations on two channels-a conical-shaped nanopore and the transmembrane pore of an α-hemolysin-under both equilibrium and nonequilibrium conditions. The simulations reveal substantial couplings between the motions of cations and anions, which are effectively captured by the collective coordinate in the model. Although the two channels exhibit very different linear ranges in the I-V curves, in both cases the channel conductance at small voltages is in reasonable agreement with the prediction from the equilibrium simulation. The simulations also suggest that channel charges, rather than geometric asymmetry, play a more prominent role in current rectification.

Figure 1

(a) Side view of the periodic cell (82 Å × 82Å × 84 Å) of the model nanopore system. The front-half of the channel and the membrane is removed to reveal the channel interior. K⁺ and Cl⁻ ions are drawn as spheres. (b) The unit cell (∼59 Å × 59Å × 94 Å) of the α-hemolysin system, with the cis side up. The protein consists of seven monomers. Both images were rendered using the VMD program (32).

Figure 2

The trajectories of the collective coordinate Q (in unit of elementary charge e) in the equilibrium simulations of the model nanopore (a) and the α-hemolysin pore (b), obtained using Eq. 23. Also shown are the trajectories of Q_K and Q_Cl arising from K⁺ and Cl⁻ ions, respectively.

Figure 3

Mean-squared displacements (MSDs) calculated from the equilibrium trajectories Q(t), Q_K(t), and Q_Cl(t) shown in Fig. 2 for the model nanopore (a) and the α-hemolysin pore (b). (Solid lines) Linear fits for the data between t = 200 ps and t = 400 ps in the MSD curve for the model nanopore (a), and between t = 1000 ps and t = 2000 ps for the α-hemolysin pore (b).

Figure 4

The observed (K⁺, Cl⁻, and total) currents at each applied voltage in the nonequilibrium simulations of the model nanopore (Table 1). (Solid line) Linear I-V curve predicted from Eq. 18, with the value of D_Q obtained from the equilibrium simulation. (Upper inset) Closeup view of the data at small voltages.

Figure 5

Concentrations of K⁺ (left panels) and Cl⁻ (right panels) ions within a cylinder of 10 Å radius around the channel axis as a function of the z position, in the simulations of the model nanopore with the indicated voltages. The narrowest constriction of the channel (Fig. 1a) is at the entrance with z = −15 Å. (Dashed lines) The corresponding ion concentrations in the equilibrium simulation.

Figure 6

Currents at each applied voltage in the nonequilibrium simulations of the α-hemolysin pore (Table 2). (Solid line) Linear I-V curve predicted from Eq. 18. (Upper inset) Closeup view of the data at small voltages.