Simple moment-closure model for the self-assembly of breakable amyloid filaments
- PMID: 23442904
- PMCID: PMC3566462
- DOI: 10.1016/j.bpj.2012.12.039
Simple moment-closure model for the self-assembly of breakable amyloid filaments
Abstract
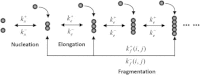
In this work, we derive a simple mathematical model from mass-action equations for amyloid fiber formation that takes into account the primary nucleation, elongation, and length-dependent fragmentation. The derivation is based on the principle of minimum free energy under certain constraints and is mathematically related to the partial equilibrium approximation. Direct numerical comparisons confirm the usefulness of our simple model. We further explore its basic kinetic and equilibrium properties, and show that the current model is a straightforward generalization of that with constant fragmentation rates.
Copyright © 2013 Biophysical Society. Published by Elsevier Inc. All rights reserved.
Figures


Similar articles
-
A Kinetic Model for Cell Damage Caused by Oligomer Formation.Biophys J. 2015 Oct 6;109(7):1338-46. doi: 10.1016/j.bpj.2015.08.007. Biophys J. 2015. PMID: 26445435 Free PMC article.
-
The role of prefibrillar structures in the assembly of a peptide amyloid.J Mol Biol. 2009 Oct 16;393(1):214-26. doi: 10.1016/j.jmb.2009.06.026. Epub 2009 Jun 12. J Mol Biol. 2009. PMID: 19524594
-
An analytical solution to the kinetics of breakable filament assembly.Science. 2009 Dec 11;326(5959):1533-7. doi: 10.1126/science.1178250. Science. 2009. PMID: 20007899
-
Fitting neurological protein aggregation kinetic data via a 2-step, minimal/"Ockham's razor" model: the Finke-Watzky mechanism of nucleation followed by autocatalytic surface growth.Biochemistry. 2008 Feb 26;47(8):2413-27. doi: 10.1021/bi701899y. Epub 2008 Feb 5. Biochemistry. 2008. PMID: 18247636 Review.
-
Modelling amyloid fibril formation kinetics: mechanisms of nucleation and growth.J Phys Condens Matter. 2013 Sep 18;25(37):373101. doi: 10.1088/0953-8984/25/37/373101. Epub 2013 Aug 14. J Phys Condens Matter. 2013. PMID: 23941964 Review.
Cited by
-
Protein Polymerization into Fibrils from the Viewpoint of Nucleation Theory.Biophys J. 2015 Nov 17;109(10):2126-36. doi: 10.1016/j.bpj.2015.10.010. Biophys J. 2015. PMID: 26588571 Free PMC article.
-
Measurement of Tau Filament Fragmentation Provides Insights into Prion-like Spreading.ACS Chem Neurosci. 2018 Jun 20;9(6):1276-1282. doi: 10.1021/acschemneuro.8b00094. Epub 2018 Apr 8. ACS Chem Neurosci. 2018. PMID: 29590529 Free PMC article.
-
Single-Molecular Heteroamyloidosis of Human Islet Amyloid Polypeptide.Nano Lett. 2019 Sep 11;19(9):6535-6546. doi: 10.1021/acs.nanolett.9b02771. Epub 2019 Aug 29. Nano Lett. 2019. PMID: 31455083 Free PMC article.
-
A Kinetic Model for Cell Damage Caused by Oligomer Formation.Biophys J. 2015 Oct 6;109(7):1338-46. doi: 10.1016/j.bpj.2015.08.007. Biophys J. 2015. PMID: 26445435 Free PMC article.
-
Statistical mechanical treatments of protein amyloid formation.Int J Mol Sci. 2013 Aug 23;14(9):17420-52. doi: 10.3390/ijms140917420. Int J Mol Sci. 2013. PMID: 23979423 Free PMC article. Review.
References
-
- Prusiner S.B. Molecular biology of prion diseases. Science. 1991;252:1515–1522. - PubMed
-
- Dobson C.M. Protein folding and misfolding. Nature. 2003;426:884–890. - PubMed
-
- Ghahghaei A., Faridi N. Structure of amyloid fibril in diseases. J. Biomed. Sci. Eng. 2009;2:345–358.
-
- Morris A.M., Watzky M.A., Finke R.G. Protein aggregation kinetics, mechanism, and curve-fitting: a review of the literature. Biochim. Biophys. Acta. 2009;1794:375–397. - PubMed
-
- Chiti F., Dobson C.M. Protein misfolding, functional amyloid, and human disease. Annu. Rev. Biochem. 2006;75:333–366. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

